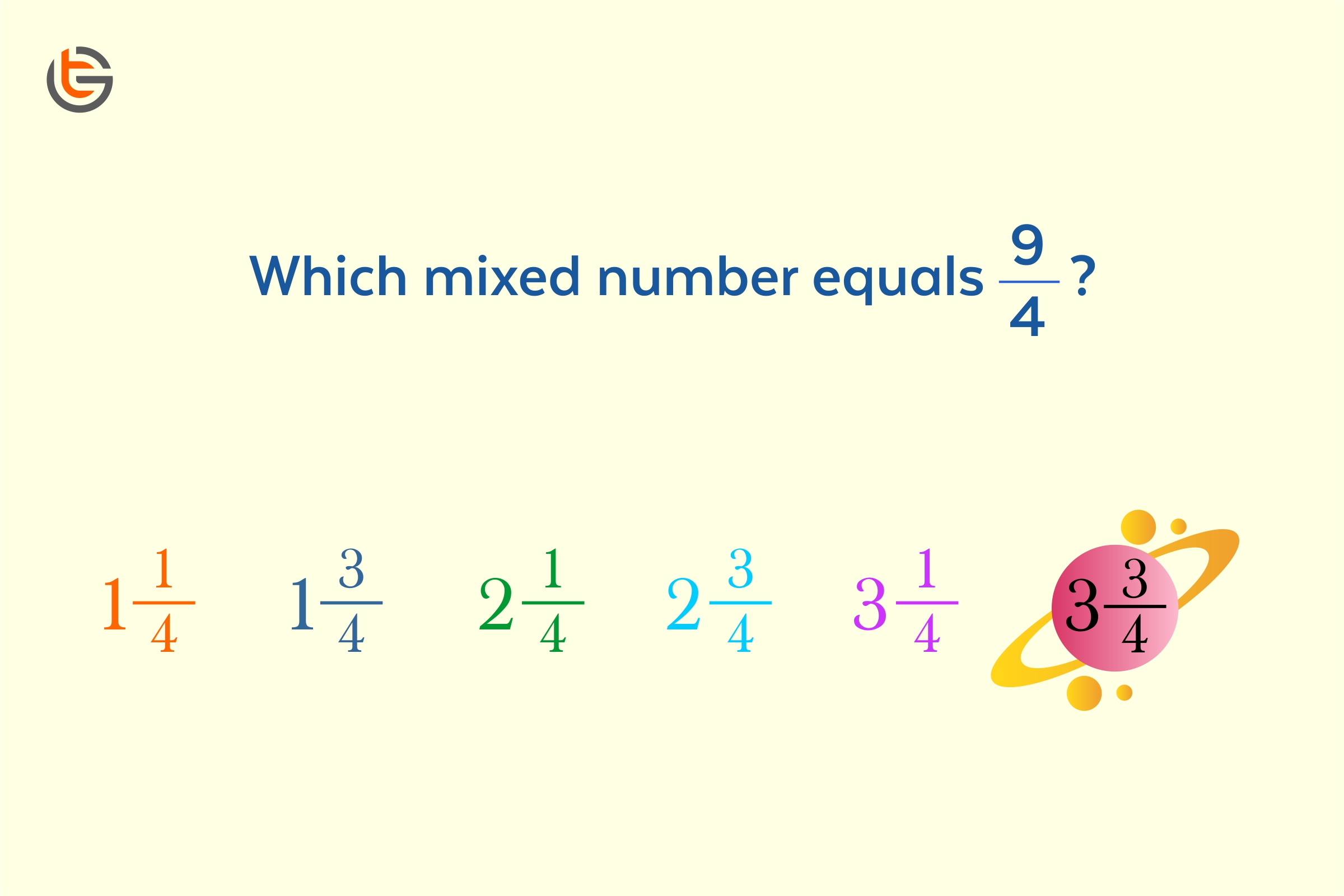Category: Mathematics Questions

Mixed Number: Mixed number commonly known as a mixed fraction is a mathematical expression that comprises a whole number as well as a fraction.

For example:

3\frac{1}{2},4\frac{4}{7},5\frac{8}{9}

Parts of a Mixed Fraction

There are basically three parts of a mixed fraction: whole number, numerator and denominator.

For example: Consider the mixed fraction 7\frac{{23}}{{37}}

Here, 7 is the whole number and \frac{{23}}{{37}} is a fraction. 23 is the numerator and 37 is the denominator.

It is the other representation form of improper fraction.

Types of fractions

There are mainly two types of fractions:

• Proper fraction: A fraction is called proper fraction when numerator is less than denominator. These types of fractions are always less than 1.

For example: \frac{7}{{10}}

Here 7 (numerator) is less than 10 (denominator). So, this is termed as proper fraction.

• Improper fraction: In a fraction, when numerator is greater than denominator it is known as improper fraction. These types of fractions are always greater than 1.

For example: \frac{7}{3}

Here 7 (numerator) is greater than 3 (denominator). So, it is an improper fraction.

Only an improper fraction can be converted into a mixed number and vice versa.

Steps to convert improper fraction to mixed fraction or number?

Follow these steps to convert improper fraction into a mixed number.

Step 1: Divide numerator by denominator. Here numerator becomes dividend and denominator become divisor (d).

Step 2: Make a note of quotient (q) and reminder (r).

Step 3:  Now, your mixed number is   q\frac{r}{d}

Let’s practice it with the help of an example:

Problem: Convert \frac{{18}}{7} into mixed number

Step1: Taking 18 as dividend and 7 as divisor, perform the division.

Step 2: On dividing 18 / 7, quotient is 2 and remainder is 4.

Step 3:  So your mixed fraction is 2\frac{4}{7}

This can also be written as 2+\frac{4}{7} where 2 is the whole number and  \frac{4}{7}  is the fraction part.

How to convert mixed number into a fraction?

A mixed number can only be converted into an improper fraction. Here are the steps.

Step1:  Multiply the whole number part of the mixed number with the denominator.

Step2: Now add the numerator to the product received in step 1.

Step3: Now the number received in step 2 will become your new numerator of the fraction. The denominator will remain the same.

Problem: Convert 5\frac{8}{7} into mixed number

Here 5 is the whole number, 8 is the numerator and 7 is the denominator.

Step1: Multiply the whole number with numerator.

5 x 7 = 35

Step2: Add 8 (numerator) and 35 (answer of step 1)

8 + 35 = 43

Step3: Your fraction becomes   \frac{{43}}{7}

Why mixed fractions?

Mixed fractions hold a very significant role in our daily lives. It’s easier for us to say that we have eaten 1\frac{3}{4} apples rather than saying   \frac{7}{4}  apples.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Mass: Mass is the amount of matter present in any physical object.  Usually mass and weight are two different terms as the weight gets affected by gravity. The mass of the object remains the same whereas the weight of the object may change from one place to another. But for elementary classes, we assume everything on the surface of the earth and the weight and mass of objects are considered as similar things.

SI units or standard units of mass

According to the metric units or standard units, Kilogram is used to measure mass. It is represented as kg. The imperial or old units of mass include pound, stone, etc. But as per international standards, Kilogram (kg) is the accepted unit for mass.

To measure heavy items or large masses such as stones, bricks, the units used are Kilograms and Tonne. For lighter items like medicines, chips, etc, we use smaller units such as grams (g) or milligrams (mg).

How to measure Mass?

There is various equipment available in the market to measure the mass of any object. For example digital scales, spring scales, balance scales, kitchen scales and bathroom scales.

Book Your 60-minutes Free Trial class NOW!

Conversions of standard units of Mass

To perform calculations and conversions, it’s important to understand the relationship between different units of mass.

1 gram (g) is equal to 1000th part of the kilogram. We can represent the same in an expression like

1 kg = 1000 g

Further 1 milligram is equal to 1000th part of a gram. So, the expression becomes

1 g = 1000 mg

Apart from Kilogram (kg), gram (g) and milligram (mg), there are several other units as well. Have a look.

Kilogram (kg)	1000 g
Hectogram (hg)	100 g
Decagram (dag)	10 g
Gram (g)	1 g
Decigram (dg)	0.1 g
Centigram (cg)	0.01 g
Milligram (mg)	0.001 g

 

By looking at the table, we can see that each entry is 10 times the lower one.  We perform multiplication or division depending on whether we want to convert into lower values or higher values respectively.

Some other higher units used for measuring heavy mass are Quintal and metric Tonne.

100 kilogram (Kg) = 1 quintal

1 metric ton (t) = 1,000 kilograms (kg)

We can also put in this way

1 t = 10 quintal = 1,000 kg = 1,000,000 g

Book Your 60-minutes Free Trial class NOW!

Let’s learn how to conversion of units in mass?

Problem 1: Convert 78 kg into grams?

From the above table, we know that 1 kg = 1000 g;

When we convert a higher unit into a lower unit, we perform multiplication.

So, 78 kg = 78 x 1000 g

= 78000 g

Let’s take another example

Problem2:  A basket of apples weights 45 Kg. There are 100 apples in one basket. Find the weight of one apple.

Here weight of basket is equal to weight of 100 apples. So,

The weight of 100 apples = 45 Kg

Weight of one apple = 45 / 100 = 0.45 kg

Writing 0.45 kg doesn’t look great. Let’s convert it into grams.

0.45 x 1000 = 450 g (1 kg = 1000 g)

The weight of one apple is 450 grams.

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Book Your 60-minutes Free Trial class NOW!

Value: Value in math is a mathematical object which is definite. In other words, value can also be termed as the answer received after performing certain math operations or calculations.

For example: The value of 3 + 9 = 12

Or the value of 34 + 7 is 41.

Types of values

There can be multiple types of values in maths. These are

• Value of expression:

The answer received by solving a particular mathematical expression or statement by performing computations.

For example:

Find the value 300 + 45 – 90?

Here the value of this expression would be 255.

• Value of variables/constants:

When variables or constants are assigned a definite number (mathematical object), it becomes its value.

For example:

• The value of a constant number π is 3.14
• The value of variable x in any algebraic expression.

 

• Value of a function:

When definite mathematical objects are assigned to the arguments of a function, the value of the function is obtained.

f (x)= x + 50.

So, when we assign x = 10, f (10) = 10 + 50 = 60.

60 becomes the value of function.

Let’s discuss some practical applications of the term ‘value’.

As per the number system there are three different types of values for a given digit in a number. These are:

Place Value:

Place value refers to the value of the place of the given digit in the number system.

For example: Place value of 9 in 697 would be tens or 10s. Similarly, the place value of 6 in the same number would be hundreds or 100s.

Face Value:

The face value of any digit is the digit itself. It has nothing to do with the place of that number. The face value is irrespective of its location on the number chart.

For example: The face value of 4 in 4,568 is 4.

Value:

The value of any digit in a number is how much it is worth depending on its placement in the number chart.  We calculate the value of any given digit in a number by multiplying place value and face value.

So, to get the value of 6 in 78,691; we first need to find place value and face value and then get their product.

Place value of 6 = 100s (hundreds)

Face value of 6 = 6 (six)

Value of 6 in 78,691 = Place value * Face value

= 100 * 6

= 600 or six hundreds

Mean Value

We often encounter this term in statistics and data handling. Mean value is finding the average of the set of given numbers.

How to calculate mean value of a set?

To calculate the mean value of the set, first add all the numbers and then divide the sum by the total number of items in the set.

For example: Suppose your set is {10, 20, 25, 45, 50}

To find the mean value:

Step 1: Add all the numbers 10 + 20 + 25 + 45 + 50 = 150

Step2: Now divide 150 with total number of items in the set i.e. 5

150 / 5 = 75

So, the mean value of set is 75.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Cubed Number: The final answer received by multiplying a whole number by itself three times is called cubed number or cube number.

For example: 11 x 11 x 11 = 1331

1331 is called the cube of 11.

Representation

There are two ways to represent a cube number. Let’s check.

Way 1:  Expanded Form

Here you write the number in the multiplication form. Let’s check few examples

a  x a x a

7 x 7 x 7

Way 2: Superscript Form

For a cube number, represent the number with 3 as superscript. Here are a few examples

a³ 

7³

How to cube a number?

To find cube of a number

Step 1: First multiply it by itself. This is also known as square of a number.

Step 2:  Now again multiply the same number with the result obtained in Step1.

So as per these steps, let’s find the cube of 27.

Step 1: 27 x 27 = 729

Step 2: 729 x 27 = 19638

So, the cube of 27 is 19638. This can also be written as

27³  = 27 x 27 x 27 = 19638

Let’s take another example

22³  = 22 x 22 x 22 which turns out to be 10648

Have a look at cubes of first 10 natural numbers

1³ = 1 x 1 x 1 = 1

2³ = 2 x 2 x 2 = 8

3³ = 3 x 3 x 3 = 27

4³ = 4 x 4 x 4 = 64

5³ = 5 x 5 x 5 = 125

6³ = 6 x 6 x 6 = 216

7³ = 7 x 7 x 7 = 343

8³ = 8 x 8 x 8 = 512

9³ = 9 x 9 x 9 = 729
10³ = 10 x 10 x 10 = 1000

What is a perfect cube?

If a number can be broken into a product of three same numbers, it is called a perfect cube.

Find if a number is a perfect cube or not

Perform prime factorization of the number. If the factors can be grouped into three exact sets of similar numbers, only then it’s a perfect cube.

For example:

• 1700 = 17 x 10 x 10

1700 is not a perfect cube as it has only two 10’s and one 17.

• 1728 = 12 x 12 x 12

1728 is a perfect cube as it is made by multiplying 12 three times.

Properties of cube numbers

1. When an even number is cubed, the answer is also even. For example: 14 x 14 x 14 = 2774. 14 and 2774 both are even numbers.
2. When an odd number is cubed, the result is also odd. For example: 13 x 13 x 13 =2197. Here, 13 and 2197 both are odd numbers.
3. The cubes of numbers ending in 1,4, 5, 6 and 9 also have the same number at the unit’s place. For example: In, 14 x 14 x 14 = 2774, 14 and 2774 both end in 4.
4. If we add the cubes of first n natural numbers, the answer is equal to all the numbers added together and then squared.

1³ + 2 ³ + 3³ + … + n³ is equal to (1 + 2 + 3 + … + n)²

Example:  Let’s add cubes of first 5 natural numbers
1³ + 2 ³ + 3³ + 4³⁺ 5³

= 1 + 8+ 27 + 64 + 125

= 225

This is same as (1 + 2 + 3 + 4 + 5)² = (15) ² = 225

‘*’ is known as star or asterisk. It is an arithmetic operator meaning multiplication or multiply. The result of applying this operator (multiplication) on two numbers gives a product. The two values that are multiplied are called multiplicand and multiplier. These numbers are also called factors of the product.

For example:

a * b = c;

Here, ‘a’ is the multiplicand and ‘b’ is the multiplier and ‘c’ is known as the product.

‘a’ and ‘b’ are also known as factors of ‘c’.

a * b is also read as  ‘a’ times ‘b’ or ‘a’ multiplied by ‘b’ or ‘a’ into ‘b’.

Ways to represent multiplication

There are three ways by which you can represent multiplication.

• a * b
• a x b
• a . b

In computer and coding languages, using the operator ‘x’ could be confusing with the letter ‘x’ of the alphabet.  So, here asterisk (‘*’) is used to represent multiplication. There is a reason behind that. Historically the character set in the computing languages was small such as ASCII, which lacked multiplication sign. Though other signs like ‘+’ and ‘-‘were present. But, every keyboard had ‘*’ and ‘.’ symbols present which later on became the multiplication sign for the computers.

‘x’ or  ‘*’? Which is better?

In higher classes, when algebra is introduced ‘x’ stands for variable values as well. It may be confusing to use ‘x’ as multiplication symbol as well as ‘x’ as a variable. To keep this confusion at bay, we prefer ‘*’ asterisk.

What is multiplication?

Multiplication means adding a number repetitively till a given number of times.

m * n = n + n + ….. + n (m times)

Let’s understand this with a problem:

Problem 5 * 13 = ?

This means that we need to add 13 five times, or it is same as 13 + 13 + 13 + 13 + 13 = 65.

Doing a ‘ * ‘ is a quick way of performing addition.

Let’s understand some basic rules on ‘*’

• Any number when multiplied by zero, the product turns out to be zero. When any of the multiplicand and multiplier turns out to be zero, the output is zero.

For example: 0 * 89 = 0

• Any number when multiplied by 1 gives the number itself.

For example: 89 * 1 = 1

• The answer (product) of two numbers remains the same irrespective of the order they appear in the expression.

For example:  89 * 12 is same as 12 * 89

• When a number is multiplied by any multiple of 10, the product is the same number with number of zeros from the multiple of 10 appended to it.

For example: 200 * 100 =?  Here there are two zeros in 100, these zeros get appended to 200 which becomes the product.

So, 200 * 100 = 20000

• If a number is multiplied by 2, it means the number is getting doubled.

For example: 45 * 2 = 90

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Factor

Factor is a number that divides a given number completely and gives remainder zero. So, a factor is the divisor of the given number. Also, when we multiply two numbers to find the product, the two numbers that are multiplied are the known as the factors of that product.  The factors of a number are the ones that completely divide it into equal parts.

For example:

13 x 2 = 26;

Here 13 and 2 are the factors of 26.

 

What does the word ‘factor’ means?

Factor is a Latin word that means ‘a performer’, ‘a maker’ or ‘a doer’. The practical applications of factors involve when you aim to divide something into equal parts. Knowledge of factors is also beneficial when you are making calculations while exchanging money, travel or understanding time.  Whether it’s arranging essentials in a box or finding patterns, factors are an important part of our everyday lives.

How to find factors of a given number?

To get the factors of a given number, there are two approaches namely multiplication and division.

Method 1: Multiplication

Here you need to find all the combinations where the given number can be expressed as the product of two numbers. All the unique numbers involved (multiplicands and multipliers) are known as the factors of that number.

For example:

Problem: Find out the factors of 18 using multiplication method.

First, we need to find all the combinations where 33 can be expressed as the product of two numbers.

1 x 33 = 33   or, 33 X 1 = 33

11 x 3 = 33    or, 3 x 11 = 33

So, the factors of 33 are 1, 3, 11 and 33.

Method 2: Division

Using division method, list down all the numbers less than or equal to the given number.

• Starting from 1, start dividing each number with the given number.
• Keep tracking the numbers that give zero as the remainder.
• These divisors are the factors. A factor is completely divisible by the given number.

For example:

Problem: Find the factors of 36 using division method.

Here, we need to divide 36 with every number starting from 1 to 36.

So, on dividing with 1, 2, 3, 4, 6, 9, 12, 18 and 36, remainder comes out to be zero.

Hence, these are also known as the factors of 36.

Properties of Factors

• There is a finite set of factors for every number.
• Except zero and 1, every number has at least two factors, 1 and the number itself.
• Factors are always Integers. They are never fractions or decimals.
• For all even numbers, 2 is always a factor.
• For all numbers ending in 0 and 5, 5 is always a factor.
• You can use multiplication and division methods to determine factors.

Prime Numbers

The numbers those have exactly two factors, 1 and itself are called prime numbers. This means you can only divide this number by itself and 1.

For example: 11 has just two factors 1 and 11.

Some examples of prime numbers are 2, 3, 5, 7, 11, 13 etc.

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development