Category: Mathematics Questions

To understand this, let us take an example from our daily life to explain this concept. 

Suppose Harry went shopping for groceries at a supermarket. There he noticed that the discount on different items was dependent on the price range of that item.  

He wondered how the price and discount were related. 

In this case, the price is dependent on another function that is cost.  

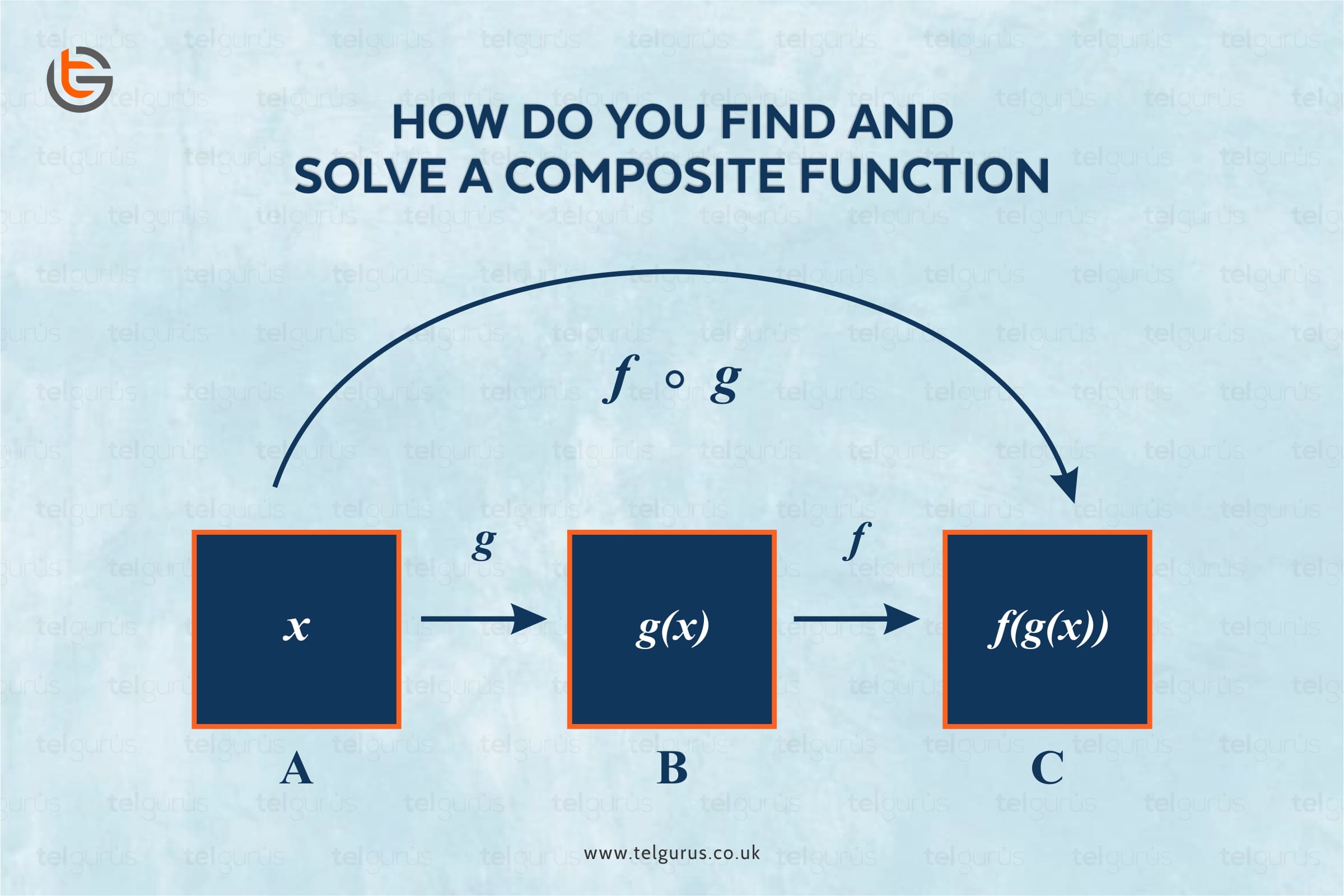
So, one function is dependent on another function. A function that depends on any other function is called a composite function.  Composite functions are functions within the functions.  

Suppose we are given two functions, with the help of these two functions we can create another function  by composing one function into the other. 

 It is generally a function that is written inside another function.   

Let us clear the concept with the help of an example.  

Example  

Let’s suppose that  

\displaystyle f(x)={{x}^{3}}  and g ( x )  = x + 6 , defined for all real numbers .  

We need to solve the equation f (g ( x )) = 125. 

f(g(x)) is usually spoken as “f of g of x”. 

Firstly, we must find the composite function f( g ( x ))  in  terms  of  x  before we solve it. 

In order to do this, we can break down the function in the following way:  

f (g ( x ))  = f  [ g ( x )  ] 

              = f  ( x  + 6 )  because  value of  g ( x )  is   x  +  6  

Now we can see that we have broken down f g ( x )  into a function of g  with in a function  of  f. 

It’s time to replace ‘x’ in \displaystyle f(x)={{x}^{3}} with  x + 6 

 That is  \displaystyle f(g(x))={{(x+6)}^{3}} 

We can now use the above function to rearrange and solve for f g ( x )  = 125 

 Therefore \displaystyle {{(x+6)}^{3}}=125

                    x + 6  =  ³√125

                    x + 6  = 5 

                    x  =  5 –  6 

                   x =  -1  

Here, one thing is to be kept in mind is that the value of composite function f (g ( x )) is  not the same as the value of the composite function  g (f ( x )). 

Both functions have different values. We can also denote these functions as ( f o g  )  ( x )  where o is a small circle symbol. 

 Note that, we cannot replace o with (.) because dot will refer to the product of two functions.  

Few properties of composite function  

• The function composition of one-to-one function is always one-to-one.  

• The function composition of two onto functions is always onto. 
•  The inverse of the composition of two functions f and g is equal to the composition of the inverse of both the functions i.e.  \displaystyle {{(\text{ }f~o\text{ }g\text{ })}^{{-1}}}~\left( {\text{ }x\text{ }} \right)~\text{ }=~~\text{ }(\text{ }g{{~}^{{-1}}}~o~~\text{ }f{{~}^{{-1}}}~~)~~\left( {\text{ }x\text{ }} \right). 
• Composite functions are not commutative, i.e. g o f (x) is  not equal to  f o g (x). 
• Composite functions are associative , i.e. taking three functions f, g and h:  ( f o g ) o h  =  f o ( g o h )  

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Differentiation in mathematics is the rate of change of a function with respect to a variable.  Differentiation is one of the two key areas of calculus apart from Integration. 

Differentiation i.e.  calculating the derivative requires the use of basic definition very rarely. But, to differentiate a function the rules of derivatives must be known.  

The derivative of a constant function is always zero.  

Let  y = f (x ) be any function. We can explain it as the measure of the rate at which the value of y changes with respect to the change of the variable x. 

It is read as the derivative of function ‘f’   with respect to the variable x. There are different methods to find the derivatives of the given functions. These methods are: 

• Product Rule  
• Chain Rule  

• Quotient Rule  

Now the question is how we will come to know whether we have to use chain rule or product rule to find the derivative of the given function. 

These are two really useful rules for differentiating functions. We use the chain rule when differentiating a composite function that is a “function of a function”, like f [ g ( x )  ] in general. 

We use the product rule in differentiation when two functions are multiplied together such as f ( x )  * g ( x ) in general . Here in this case there are two functions not function of a function. Let us clear the difference between these two methods with the help of example:  

Example: f ( x )  = sin ( 3 x )  

This is an example of a composite function means a “function of a function” or “function within a function”. 

 A function that depends on any other function is called a composite function.   

Suppose we are given two functions, with the help of these two functions we can create another function by composing one function into the other. 

 It is generally a function that is written inside another function.  The two functions in the above example are as follows: 

# Function one takes x and multiplies it by 3.  

#Function two takes the sine of the answer given by the function one.  

So, we use chain rule to differentiate these types of functions that means composite functions where one function contains another function.  

To the contrary, if the given function is of the form say,  

\displaystyle f(x)={{x}^{2}}\cos \,(x)

In this case we will use the product rule because here we have two separate functions multiplied together.   

• ‘ \displaystyle {{x}^{2}}’ (first function )takes only x and has nothing to do with another function.  
• cos ( x ) takes the cosine of x and is not dependent in the first function ( \displaystyle {{x}^{2}}). 

But one thing to be kept in mind here is that they both are separate functions one do not rely on the answer to the other.  

So, product rule is used when two different functions are given. One function is not dependent on the other function.  

From above discussion we can conclude that we should use chain rule when you see functions to be differentiated within each other and use the product rule when you see functions to be differentiated in multiplication that is when the two functions are in product form.  

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Before finding the prime factors of 56 we must know what the term ‘factors’ mean. When two numbers are multiplied together, and the result is a given number, then the two numbers are called factors of that number. 

Factors of 56 are all such numbers that completely divides the number 56 and when multiplied in pairs give the product as 56. 

These factors of 56 are positive numbers but can be negative as well. 

All such numbers that divide 56 without any remainder are factors of 56. Only whole numbers and integers can be the factors of a number.  

So, the factors of 56 are 1 , 2 , 4 , 7 , 8 , 14 , 28  and 56. This means that all these numbers divide 56 completely.  

 Important points to remember 

• Decimals and fractions (anything that is not integer) cannot be the factors of any number.  

• When a number is a factor of the given number, then its additive inverse is also a factor of the given number. For example, since 4 is a factor of 56, – 4 is also a factor of 56.  

Now, before finding the prime factors of 56 we must know what we mean by prime numbers. 

Prime numbers are the basic building blocks of all the numbers. They can’t be divided by any number apart from 1 or themselves.  

That means a prime number is a number that has exactly two factors, 1 and the number itself.   

Prime factorization means to represent any given number as a product of prime numbers. 

There are various methods for finding the prime factors of a number.  

• Division method 
• Factor tree method  
• Division method  

 Prime Factorization of 56 by division method  

We know that 56 is a composite number and it will be having factors that can be further broken into prime numbers. Now let us know how to find out the prime factors of 56.  

Step 1:  Let’s divide the number 56 with the smallest prime number i.e. 2  

Therefore, 56 / 2 = 28 

Step2:  Again, divide 28 by 2 and the process goes on.  

 28 / 2 = 14 

  14 / 2  = 7  

Step 3: Now, if we divide 7 by 2 we will get a fractional number, which cannot be a factor. So, we move to next prime number that divides 7 completely which is 7 itself.  

   7  /  7  =   1  

Step 4:  We have received 1 at the end of the division process and so that we cannot proceed further.  

So, the prime factors of 56 are 2  x 2 x 2 x 7  

56 as the product of its prime factors by division method = 2 x 2 x 2 x 7 where 2 and 7 both are prime numbers.  

Prime Factorization  

It is just like the division method. The only difference is that presentation. 

2	56
2	28
2	14
7	7
	1

 

So, prime factorization becomes 56 = 2 * 2 * 2 * 7. 

Prime Factorization of 56 by Factor Tree Method  

Prime factors of 56 can also be found by making a factor tree. Here, we need to count the last most nodes or leaves of the tree.  

Thus, the prime factors of 56 are 2 x 2 x 2 x 7   by factor tree.  

From the above two methods we can conclude that 56 as the product of its prime factors = 2 x 2 x 2 x 7 . 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Every expression in algebra or a formula comprises of more terms, variables and constants.  

The main subject is always kept on the right hand side and all the dependent variables are kept on left hand side.  

The values for the subject are calculated by substituting the values in right hand side of the expression. 

 For example:  

We know that, Speed = Distance/ Time or S = D/T 

In case we need to calculate Distance, we need to rearrange the formula to get Distance on left hand side and rest everything on right hand side. 

S = D / T 

On multiplying T (Time) on both the sides, we get 

S * T = D / T * T 

S * T = D 

Or, D= S * T 

Now, we get a single variable on the left hand side i.e. Distance.  

This way we can change the subject.   

• Involving squares/roots 

If A is area of a square with side S, we know that 

A = S2 

To calculate side, we will take square root on both the sides  

√A = √S2 

⇒ S = √A 

• Involving fractions  

If C stands for degree Celsius and F stands for Fahrenheit scale, we know the conversion rule i.e. 

(C – 0)/ 100  = (F -32)/ 180 …………………………….    (1) 

With this formula we can easily switch between the subjects and calculate what is desired.  

To convert Celsius scale to Fahrenheit scale, we will perform mathematical actions in such a way that F should be on one side and take the rest terms on the other side. 

Multiplying 180 on both sides on equation (1) 

C/100 * 180 = F-32 

Now, adding 32 on both sides and simplifying  

9C/5  + 32 = F 

So, the new temperature becomes F = 9C / 5  + 32. 

Similalr we can change the subject from F to C, by performing reverse operations which gives  

C = (F -32)* 5/9 

Let’s solve them using some practical examples 

Example1: Find the height of a cuboidal box, if its length is 10 cm, breadth is 45 cm and volume is 9000 cu cm.  

Solution: We know that V =  L *B *H 

But, here we need to find the value of h or height or make the main subject. 

In the above formula, we will divide both the sides with l and b 

Which gives us  

V/ (L *B) = H 

Substituting the values here, we get 

9000 / (45 * 10) = H 

H = 20 cm 

Height comes out to be 20 cm.  

Example2: Find the radius of a circle whose area is 314 cm2.  

Solution: We know the formula that 

\displaystyle A=\pi {{r}^{2}} where A is the area and r stands for radius. 

Here the main subject is A, we need to change the subject to r. 

For that we will divide both the sides with π  

\displaystyle A/\pi \,\,=\,\,\,{{r}^{2}}

Now taking square roots on both the sides, radius becomes  

r = √A/ π 

Now, Let now substitute the values given in the question to this derived.  

r = √(314/ 3.14) = √100 = 10 

The radius comes out be 10 cm.

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Trigonometry is one of the most important branches in mathematics and it deals with the study of the relationship between the sides and angles of right triangle. 

 Trigonometry has three most important functions which are primarily used by the students to find out the unknown value of an angle and the length of sides of a right-angled triangle.   

The names and abbreviations of these three functions are sine  ( sin ),  cosine ( cos ), Tangent ( tan ). 

These three are the primary functions and there are other three trigonometric functions which are the reciprocals of these functions.  

Cosecant  ( cosec )   is the reciprocal of  sine ,  Secant ( sec ) is the reciprocal of  cos  and Cotangent  ( cot ) is the reciprocal of tangent  In most cases we  have  used  different identities of trigonometry  on right angled triangles. 

But, can we apply these laws to other triangles also? 

We can’t apply trigonometric functions on other triangles apart from right angled triangles. But if, somehow we convert the given triangle into a right triangle then certainly we can apply and use the trigonometry formulas. 

A larger part of mathematical questions are just about transformations. So, if we want to apply trigonometric functions on non right triangles, we need to convert a part of them into right triangles without breaking any law. 

Though law of cosines and sines apply to all triangles whether right or not but their derivation is based on right triangles only. In their derivation a part of the triangle is made to be right angled and then the laws have been derived. 

When applied to non right-triangles, the Law of sines and Law of cosines are used.  

One way that you can derive these laws is to break the non – right triangle into right triangles and find the relations among the pieces.  

For non-right angled triangles, we have the cosine rule and the sine rule. In order to use these rules, we require a technique for labeling the sides and angles of the non-right angled triangle.  

In a non right-angled triangle we have to take angle A to the opposite of the side a , angle B to the opposite of side  b  and angle C to the opposite of side c  as shown in the figure. 

 

 

We use cosine rule to find the missing side when all sides and angles are involved in the question.  It may also be used to find a missing angle if all the sides of a non – right angled triangle are given.  

 The Cosine Rule  

• \displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\,\cos (A)
• \displaystyle {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\,\cos (B) 
• \displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\,\cos (C)

Where a, b, c are the sides and A, B, C are the angles of the Δ.  

The Sine Rule  

The sine rule can be used to find a missing angle or missing side when two corresponding pairs of sides and angles are involved in the question. 

The Sine Rule states that 

a / sin ( A ) =  b / sin ( B ) =  c / sin ( C )  

Where a, b and c are the sides of the triangle and A, B and C are the angles of the Δ. 

So, we can apply these sine and cosine rules of trigonometry on non-right angled triangle to find the sides or angles.

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Before finding the square root of a complex number we must know what complex numbers are.  

A complex number is the sum of a real number and an imaginary number.  

It is written generally in the form of a + ib and it is represented by alphabet z.  

Here, both a and b are real numbers.  The value ‘a’ is called the real part and is denoted by Re ( z ). 

The imaginary part is denoted by b and is represented as  Im ( z ).  

The alphabet ‘i’ is known as iota and represents the imaginary part of the complex number.  

Further iota is very helpful to find the square root of negative numbers. 

• \displaystyle i=\sqrt{{-1}}~~
• \displaystyle {{i}^{2}}=~-1~~
• \displaystyle {{i}^{3}}=i.{{i}^{2}}\Rightarrow i(~-1)=-i~~

And so on. 

The modulus of the complex number is the distance of the complex number represented as a point in the plane (a, ib). 

Here are some important points regarding complex numbers. 

• All real numbers are complex numbers but the vice versa is not true.  
• All imaginary numbers are complex numbers but vice versa needn’t need to be true. 
• The conjugate of a complex number  z  = a  +  ib   is  z  =  a   –  ib 

• The magnitude of a complex number z = a + ib  is  | z |  = \displaystyle \sqrt{{{{a}^{2}}+{{b}^{2}}}}~~

Now, let’s discuss how can we find the square root of a complex number? 

So, given below are some steps which we have to follow to find the square root of a complex number.  

Firstly , suppose   x + iy  be the square root of the complex number  a  +  ib .  Then we can say, 

 x + iy  = √ ( a + ib) 

as we have supposed  x + iy be the square root of  a + ib 

 Now squaring both sides we get , 

\displaystyle {{(x+iy)}^{2}}=a+ib

 

\displaystyle {{x}^{2}}+{{(iy)}^{2}}+2(x)(iy)=a+ib

Putting the value of  \displaystyle {{i}^{2}}=-1

\displaystyle {{x}^{2}}-{{y}^{2}}+i(2xy)=a+ib

Now, equating real and imaginary parts, we get: 

\displaystyle {{x}^{2}}-{{y}^{2}}=a   and    2xy =  b   

Now    \displaystyle {{({{x}^{2}}+{{y}^{2}})}^{2}}={{({{x}^{2}}-{{y}^{2}})}^{2}}+4{{x}^{2}}{{y}^{2}}

                                      = \displaystyle {{a}^{2}}+{{b}^{2}}

Now we have  \displaystyle ({{x}^{2}}+{{y}^{2}})=\sqrt{{({{a}^{2}}+{{b}^{2}})}} ……………….  ( 1 )  

Also ,   \displaystyle {{x}^{2}}-{{y}^{2}}=a   ………………………………. ( 2 ) 

Adding equation (  1 ) and equation ( 2 ) we get ,  

\displaystyle {{x}^{2}}=1/2(\sqrt{{({{a}^{2}}+{{b}^{2}}}})+a)=h ( say )  

Now , subtracting equation  ( 2 )  from  equation ( 1 )  we get ,  

\displaystyle {{y}^{2}}=1/2(\sqrt{{({{a}^{2}}+{{b}^{2}}}})-a)=k ( say )  

Thus, 

x  = √ h , – √ h  and  y  =  √ k , – √ k  

In this way we can find the square roots of a complex number. 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development