When do I use the chain rule and when do I use the product rule in differentiation?

Book A Demo Class

Differentiation in mathematics is the rate of change of a function with respect to a variable. Differentiation is one of the two key areas of calculus apart from Integration.

Differentiation i.e. calculating the derivative requires the use of basic definition very rarely. But, to differentiate a function the rules of derivatives must be known.

The derivative of a constant function is always zero.

Let y = f (x ) be any function. We can explain it as the measure of the rate at which the value of y changes with respect to the change of the variable x.

It is read as the derivative of function ‘f’ with respect to the variable x. There are different methods to find the derivatives of the given functions. These methods are:

Product Rule
Chain Rule

Quotient Rule

Now the question is how we will come to know whether we have to use chain rule or product rule to find the derivative of the given function.

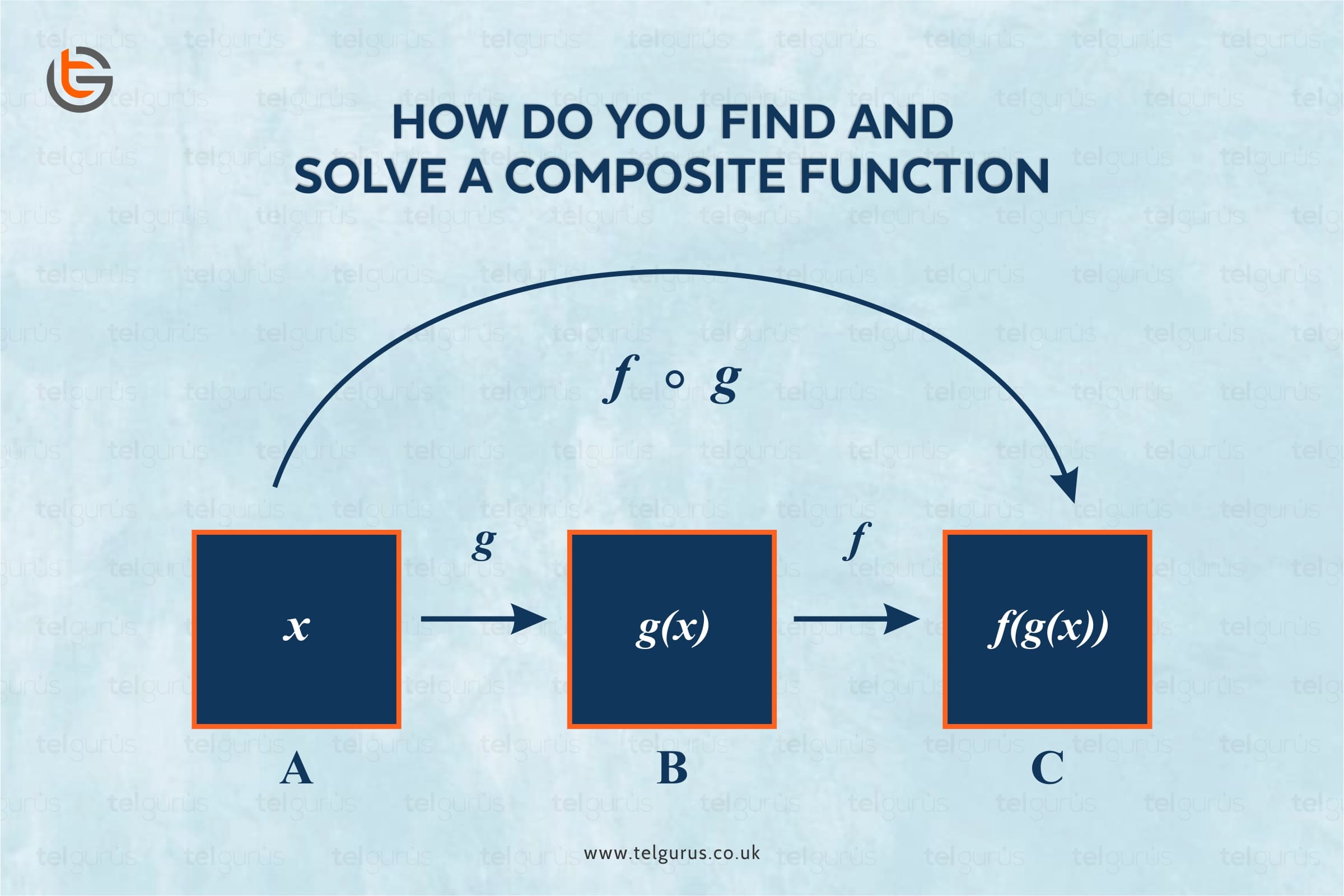
These are two really useful rules for differentiating functions. We use the chain rule when differentiating a composite function that is a “function of a function”, like f [ g ( x ) ] in general.

We use the product rule in differentiation when two functions are multiplied together such as f ( x ) * g ( x ) in general . Here in this case there are two functions not function of a function. Let us clear the difference between these two methods with the help of example:

Example: f ( x ) = sin ( 3 x )

This is an example of a composite function means a “function of a function” or “function within a function”.

A function that depends on any other function is called a composite function.

Suppose we are given two functions, with the help of these two functions we can create another function by composing one function into the other.

It is generally a function that is written inside another function. The two functions in the above example are as follows:

# Function one takes x and multiplies it by 3.

#Function two takes the sine of the answer given by the function one.

So, we use chain rule to differentiate these types of functions that means composite functions where one function contains another function.

To the contrary, if the given function is of the form say,

$\displaystyle f(x)={{x}^{2}}\cos \,(x)$

In this case we will use the product rule because here we have two separate functions multiplied together.

‘ $\displaystyle {{x}^{2}}$ ’ (first function )takes only x and has nothing to do with another function.
cos ( x ) takes the cosine of x and is not dependent in the first function ( $\displaystyle {{x}^{2}}$ ).

But one thing to be kept in mind here is that they both are separate functions one do not rely on the answer to the other.

So, product rule is used when two different functions are given. One function is not dependent on the other function.

From above discussion we can conclude that we should use chain rule when you see functions to be differentiated within each other and use the product rule when you see functions to be differentiated in multiplication that is when the two functions are in product form.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development