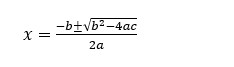Enrich your knowledge with our informative blogs
What is the most useful formulas in math?
What is the most useful formulas in math?
Turning pages of your randomly to find the most used math formulas?
Facing difficulty in revising maths problems as your formulas seems scattered?
Not anymore. TEL Gurus bring you a complete and holistic guide of maths formulas.
Just skimp through this list.
Bingo! You are ready for your exams.
Math formulas are expressions or set of rules that help you solve the mathematics problems quickly and accurately.
From Key stages to GCSE, advance level maths concepts become easy to grasp if you know the formula.
The best way to learn the formulas is Practice, Practice and Practice.
So, let’s make your maths learning more easy and fun with these exhaustive list of maths formulas.
- Number Theory
- Geometry
- Arithmetic
- Algebra
- Probability
- Combinatorics (Permutation & Combination)
- Trigonometry
- Consumer Math Formulas
- Statistics
- Calculus
1. Number Theory
1.1 Number sets
Let’s discuss all the number sets with examples
Number Sets |
||
| Number set type | Definition | Example |
| Natural Numbers | All counting numbers are natural numbers | N= 1,2,3,… |
| Prime Numbers | The numbers having exactly two factors i.e. 1 and the number itself | P= 2,3,5 ,7,11,… |
| Composite Numbers | Number having more than two factors | 4,6,8,10,12,14,… |
| Whole Numbers | All natural numbers with 0 form the whole numbers | W= 0,1,2,3,4,5,… |
| Integers | All positive and negative numbers form integers. | Z= ….,-4,-3,-2,-1,0,1,2,3,4,…. |
| Rational Numbers | Numbers that can be written in form of fractions. | Q = 1/2, 11/10, 0.3333 |
| Irrational Number | Numbers that cannot be written as fractions. | F = π, √2, .. |
| Real Numbers | Real numbers are a set of rational and irrational numbers. | R=…,−1,0,1,1.1,–√7,2,π,… |
| Complex Numbers | Any number that can be written in the form of a + ib, where a is the real part and b is the imaginary part and i stands for √-1. | C=…,−5+6i, 0, 7+9i, … |
2. Geometry Formulas
2.1 2D shapes
2D Shapes |
|||
| Shape | Variables | Perimeter | Area |
| Square | Side =s | 4s | s2 |
| Rectangle | Length= l
Breadth = b |
2(I + b) | lb |
| Circle | Radius =r | 2πr | πr2 |
| Triangle | Side1 = a
Side2 = b Side3 = c s = (a+b+c)/2 s is semi perimeter |
a +b +c | √(s(s-a)(s-b)(s-c)) |
| Right angled triangle | Base = b
Height = h Side 2 = a Side 3= c |
a +b +c | ½ * b*h |
| Parallelogram | Base= b
Height = h Other side = a |
2 (a +b ) | bh |
2.2 3D shapes
3D shapes |
||||
| Shape | Variables | Volume | Curved Surface area / lateral surface area | Total Surface Area |
| Cube | Edge = a | a3 | 4a2 | 6a2 |
| Cuboid
|
Length =l breadth=b
height =h |
lbh | 2h(I + b) | 2 (lb + bh + hl) |
| Cylinder
|
Radius of the circular base =r
Height = h |
πr2h | 2πrh | 2πr (r + h) |
| Cone | Radius of the circular base =r
Height = h Slant height = l |
1/3 πr2h | πrl | πr (l + r) |
| Sphere | Radius = r | 4/3 πr3 | 4 πr2 | 4 πr2 |
| Hemisphere | Radius = r | 2/3 πr3 | 2 πr2 | 3 πr2 |
2. Arithmetic Formulas
2.1 BODMAS
BODMAS is an acronym that stands for brackets, Order, division, multiplication, addition and subtraction.
It tells us the order to be followed while performing arithmetic calculations.
2.2 Fractions
Fractions are part of a whole.
A fraction has two parts numerator and denominator. The upper part of fraction is known as numerator and lower part as denominator.
For example: ¾ here 3 is the numerator and 4 is the denominator.
Concepts of Fraction |
|
| Proper Fraction | When numerator < denominator, the fraction is proper fraction. For example: 3/4 |
| Improper fraction | When numerator > denominator, the fraction is improper fraction. For example 8/5. |
| Mixed Fraction | A mixed fraction has both a whole number and fractional part. For example: |
| Like Fractions | Two fractions are said to be like fractions when they have same denominator. Example: 2/13 and 5/13 are like fractions |
| Unlike Fractions | Two fractions are said to be unlike fractions when they have different denominator. Example: 2/3 and 5/8 are unlike fractions |
Let a/b and c/d are two fractions where a≠b≠c≠d
2.3 Progressions
Progressions are when numbers are arranged in a particular order. There are three major types of Progressions Arithmetic Progression, Geometric Progression and Harmonic Progression.
4. Algebra Formulas
Algebraic formulas are used to calculate expressions involving variables and constants. Here is a quick revision to all the formulas
- (a + b)2= a2 + 2ab + b2
- (a – b)2= a2 – 2ab + b2
- (a + b)(a – b) = a2– b2
- (x + a)(x + b) = x2+ x(a + b) + ab
- a2 + b2 = (a + b)2 -2ab
- (a + b + c)2= a2 + b2 + c2 + 2ab + 2bc + 2ca
- (a – b – c)2= a2 + b2 + c2 – 2ab + 2bc – 2ca
- (a + b)3 = (a + b)3 = a3 + b3 + 3ab(a + b)
- (a – b)3 = a3 – b3 – 3ab(a – b)
- (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
- (a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
Here are some formulas involving exponents having same bases with different powers or different bases with same powers.
- am. an = am+n
- am / an = am-n
- (am)n = amn
- (ab)m = am. bn
- a0 = 1
- (a)-m = 1/am
Quadratic Formula
For any quadratic equation ax2 + bx + c = 0
Where x is the variable and a,b,c are constants, the roots can be calculated by using the formula
b2 – 4ac is also called determinant (D) and helps in finding the nature of the roots.
- D > 0, then the quadratic equation has two distinct real roots.
- D = 0, then the quadratic equation has two equal real roots.
- D < 0, then the quadratic equation has two imaginary roots.
5. Probability Formulas
The likelihood of an event happening is known as probability (p).
The probability of not happening an event is 1 – p.
Probability formula
P(A) = Number of favourable Outcomes / Total number of favourable outcomes
Here P(A) is the probability of an event A.
Or, it is also written as
P(A) = n (A) /n (S)
n(A) stands for number of favourable outcomes
n(S) stands for total number of events in the sample space
Let’s discuss some probability formulas for two events say, A and B.
Most useful Probability formulas |
|
| Probability Range | 0 ≤ P(A) ≤ 1 |
| Additional Rule | P(A∪B) = P(A) + P(B) – P(A∩B) |
| Complementary Addition | P(A’) + P(A) = 1 |
| Independent events | P(A∩B) = P(A) * P(B) |
| Disjoint events | P(A∩B) = 0 |
| Bayes’ Formula | P(A | B) = P(B | A) * P(A) / P(B) |
| Conditional Probability | P(A | B) = P(A∩B) / P(B) |
Let’s revise with an example:
| Q1. Calculate the probability of getting an even number on rolling a dice.
Solution: Sample space (S) = { 1,2,3,4,5,6} n(S) = 6 Let A be event of getting even number (favourable outcome) = {2,4,6} n(A) = 3 Probability of getting an even number = n(A)/n(S) = 3/6 = ½ So, the probability of getting an even number on rolling a dice is ½. |
6. Combinatorics
Let there be n things, they can be arranged in n factorial Ways.
n factorial is written as n! and can be calculated as n (n-1) (n-2)…3*2 *1.
Conventionally 0! is considered as 1.
Permutation and combination
The primary difference between permutation and combination is the order.
If the order of things matter, it’s a permutation and if it doesn’t it’s a combination.
Permutations of n things taken r at a time can be determined by:
P(n,r) = n! / (n−r)!
Combinations of n things taken r at a time can be determined by:
C(n,r) = n! / (n−r)! r! or,
C(n,r) = P(n,r) / r!
Let’s understand this with the help of an example:
| Permutation: Picking a Captain and Vice captain from a group of 10 sportspersons.P(10,2) = 10! / 8!
= 10 * 9 = 90 |
| Combination: Picking a team of 4 students from a class of 10 students.C (10,4) = 10! / 4!6!
= 10 * 9 * 8 *7 / (4* 3 *2 * 1) = 210 |
7. Trigonometry
This branch of mathematics deals with the study of triangles and relationships between its side lengths and angles.
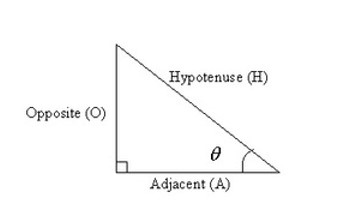
7.1 Pythagoras Theorem
In a right angled triangle,
(Hypotenuse)2 = (Base)2 + (perpendicular)2
There are six main trigonometric ratios sine, cosine, tangents, cosecant, secant and cotangent.
7.2 Basic trigonometric ratio formulas
Taking right angled triangle as base with one of the angle as θ.
sin θ = Opposite Side/Hypotenuse or, O/H
cos θ = Adjacent Side/Hypotenuse or, A/H
tan θ = Opposite Side/Adjacent Side or, O/A
sec θ = Hypotenuse/Adjacent Side or, H/A
cosec θ = Hypotenuse/Opposite Side or, H/O
cot θ = Adjacent Side/Opposite Side Or, A/H
7.3 Reciprocal Identities
In a right angled triangle with an angle θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- sec θ = 1/cos θ
- cosec θ = 1/sin θ
- cot θ = 1/tan θ
Also, tan θ = sin θ /cos θ
cot θ = cos θ/ sin θ
cos2 θ + sin2 θ = 1
7.4 Co-function Identities
The co-function or periodic identities can also be represented in degrees as:
- sin(90°−x) = cos x
- cos(90°−x) = sin x
- tan(90°−x) = cot x
- cot(90°−x) = tan x
- sec(90°−x) = cosec x
- cosec(90°−x) = sec x
7.5 Trigonometric table
Trigonometric Table |
|||||
| Angle degrees (Radians) | 0° (0°) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) |
| Sine | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cosine | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tangent | 0 | 1/√3 | 1 | √3 | ∞ |
Let’s learn with an example:
| Example: Solve (cos 30° + sin 30°) – (cos 60° + sin 60°)?
Solution: From the trigonometric table we can get the values of all the ratios cos 30° = √3/2 sin 30° = 1/2 cos 60° = 1/2 sin 60° = √3/2 Substituting the values in (cos 30° + sin 30°) – (cos 60° + sin 60°) We get, (√3/2 + 1/2) – (1/2 + √3/2) = 0 |
8. Consumer Math Formulas
8.1 Percentage
A fraction with denominator 100 is considered as percentage. The symbol “%” is used instead of over 100.
- Converting any number into a percentage
Multiply by 100%.
- Converting any percentage into a number
Remove the percentage sign and divide by 100
- Percent increase
% increase = (increase/ original value)* 100%
- Percent Decrease
% increase = (Decrease / original value)* 100%
| Q1. In the exam, John obtained 406 marks out of 500. Calculate the percentage of marks obtained by John.
Solution: % marks = (marks obtained/ total marks) * 100% = (406/500) * 100% = 81.6% John obtained 81.6% marks in the exam. |
8.2 Profit/Loss
If an item is sold above the cost price, it is said to have been sold at a profit.
Profit = Selling Price – Cost Price
Profit% = (Profit/Cost Price ) * 100%
If an item is sold below the cost price, it is said to be sold at a loss.
Loss = Cost Price – Selling Price
Loss% = (Loss/Cost Price) * 100%
Some other formulas:
Discount = List Price * Discount rate
Discount rate = discount / list price * 100%
Sale Price = List Price – Discount
Sales tax = Price of item * tax rate
8.3 Interest Calculation
Simple Interest
Simple Interest = Principal * rate of Interest * Time
Amount = Principal + Simple Inertest
Compound Interest (CI)
CI = Interest on the principal + CI at regular intervals
CI = P ( 1 + r/100)nt – P
Here,
P is principal
r is rate of interest
n is the number of times interest gets compounded annually
t is the time frame
If the principal amount is compounded annually n becomes 1.
The formula becomes:
CI = P ( 1 + r/100)t – P
Amount = P (1 + r/100)t
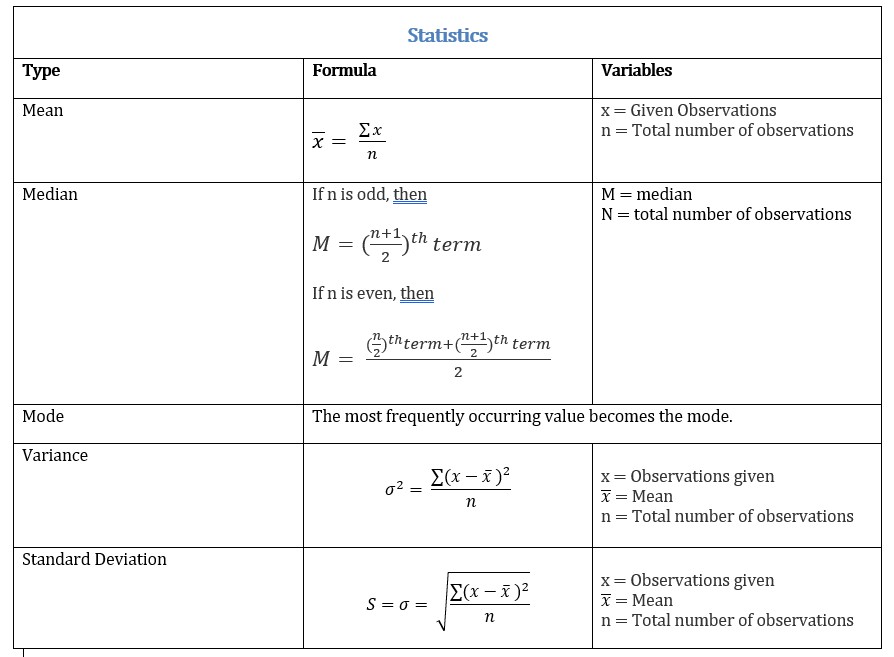
9. Statistics
When it comes to analysing and dealing with data and numbers, Statistics is used. It’s a branch of mathematics that performs the study of interpretation, collection, analysis, organization and presentation of data.
Let’s have look at most useful formulas in Statistics.
Let’s understand this with help of an example:
| Example 1: Here are the marks obtained by the students in exams = {140,150,160,150,170,150,180}. Find the mode.
Solution: Since, 150 is the only value that has the maximum frequency i.e. 3. Mode = {150} So, mode in the list is 150. |
10. Calculus
Calculus is the branch of mathematics that majorly involves the study of “rate of change” that includes convergence of infinite sequences or within a defined limit.
Differential Calculus and Integral Calculus are two major branches of Calculus. While differentiation splits area into small parts, integration does the reverse.
Let’s have a look at the common formulas related to both.
10.1 Differentiation Formulas
10.2 Integration Formulas
- ∫xn.dx = xn+1/(n+1) + C
- ∫1.dx = x + C
- ∫ex.dx = ex + C
- ∫(1/x).dx = log |x| + C
- ∫ax.dx = (ax/ln a) + C
- ∫cos x.dx = sin x + C
- ∫sin x.dx = -cos x + C
- ∫sec2 x dx = tan x + C
- ∫cosec2 x dx = -cot x + C
- ∫sec tan x dx = sec x + C
- ∫cosec x. cot x dx = -cosec x + C
- ∫a dx = ax + C
- ∫ln x dx = x.ln x – x + C
- ∫tan x dx = ln |sec x| + C
- ∫tan2 x dx = tan x –x +C
- ∫sec x tan x dx = sec x + C
- ∫cot x. dx = ln |sin x| + C
- ∫sec x dx = ln |sec x + tan x| + C
- ∫cosec x dx = ln |cosec x – cot x | + C
Where C is known as integration constant
So, get these formulas by heart and start preparing for your exams.
Good Luck!
Discover better learning pace and Flexibility
Online tuition by TEL Gurus helps you learn at your own pace and garner the flexibility to choose your preferred timeslots.
Categories
Recent Posts
- List of the qualities you should look for in your tutors?
- What is the most useful formulas in math?
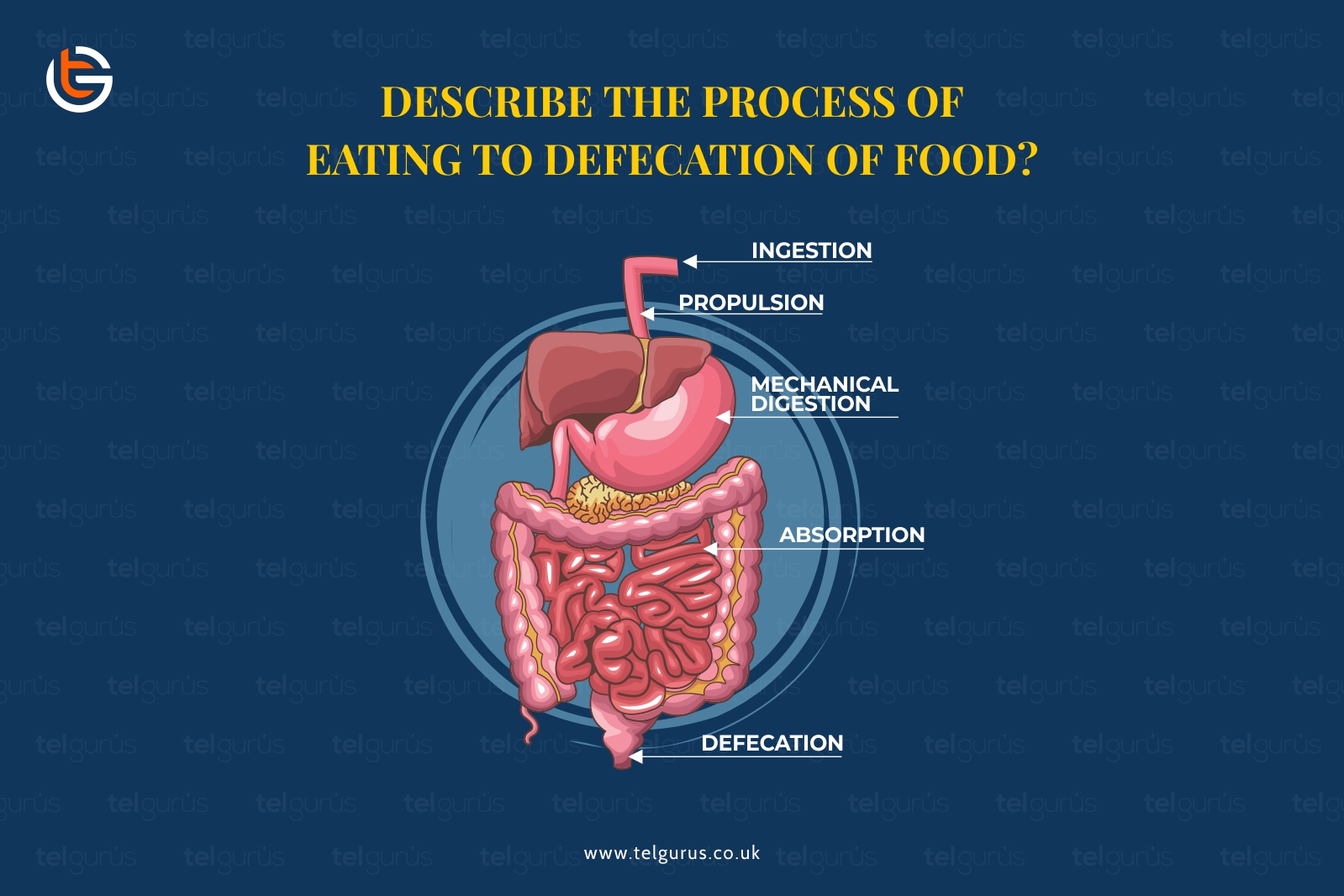
- Describe the process of eating to defecation of food?
- Difference between the natural and artificial active response by the immunology system.
- Explain the different circle theorems
- How are nerve cells adapted to their function?