Enrich your knowledge with our informative blogs
Explain the different circle theorems

A circle is the locus of all the equidistant points from a particular fixed point.
This fixed point is referred to as the centre of a circle.
The circle theorem includes the concepts of angles, sectors, tangents, circle chords, and proofs.
Let us learn about the circle theorems here only.
Circle Theorems
The different circle theorems include:
__________________________________________________________________
Theorem 1
“Two equal chords of the circle subtend equal angles at the circle’s centre.”
__________________________________________________________________
Proof of the theorem:
In ∆AOB and ∆COD,
AB=CD {because both have equal chords} ————- (1)
OA= OB= OC= OD {Circle Radii} —————- (2)
From the equation (1) and (2),
∆AOB ≅ ∆COD
Therefore by CPCT, we get
∠AOB = ∠COD
Hence Proved.
__________________________________________________________________
The Converse of Theorem 1
“If two angles subtended at the centre by two chords are equal, the chords are also of equal lengths.”
__________________________________________________________________
[REFERRING TO THE SAME IMAGE USED IN THE FIRST THEOREM]
In ∆AOB and ∆COD,
∠AOB = ∠COD (Equal angles subtended at the circle’s centre “O”) ———– (1)
OA= OB= OC= OD ———— (2)
From equations 1 and 2,
∆AOB ≅ ∆COD
Therefore, By CPCT, we get AB = PQ.
__________________________________________________________________
THEOREM 2
“The Perpendicular to a chord bisects the chord if drawn from the centre of a circle.”
__________________________________________________________________
According to the theorem, in the figure OP ⊥ AB.
Therefore, AP = PB
Proof of the theorem
In ∆AOP and ∆BOP,
∠APO = ∠BPO = 90° (OP ⊥ AB) ———— (1)
OA = OB —— (2)
OP = OP (COMMON SIDES) ——— (3)
From the equations 1, 2, and 3,
AP = PB By CPCT
__________________________________________________________________
The converse of the Theorem 2
“A straight line passing through a circle’s centre to bisect the chord is perpendicular to the chord.”
__________________________________________________________________
REFERRING THE SAME IMAGE USED IN THEOREM 2
In ∆AOP and ∆ BOP,
AP = PB (As OP bisects AB) ———- (1)
OA = OB (Radii of circle) ————- (2)
OP = OP (Common side) ————— (3)
From equations 1, 2, and 3,
∠APO = ∠BPO = 90° (By CPCT)
__________________________________________________________________
Theorem 3
“Equal chords of a circle are equidistant from the circle’s center.”
__________________________________________________________________
Construction: Join OB and OD
[REFERENCE IMAGE ONLY: Using EF instead of PQ]
Proof of Theorem
In ∆OEB and ∆OFD,
BE = ½ AB (Perpendicular to a chord bisects it) ——— (1)
DF = ½ CD ——————— (2)
Given, AB = CD
BE = DF (from equations 1 and 2)
OB = OD (Radii of the same circle)
∠OEB = ∠OFD = 90°
∆OEB ≅ ∆OFD
Hence, OE = OF (By CPCT)
__________________________________________________________________
The converse of the 3rd Theorem
“Chords of a circle that are equidistant from the centre are equal in length.”
__________________________________________________________________
REFERRING THE SAME IMAGE USED IN THIRD THEOREM
In ∆OEB and ∆OFD,
OE = OF —————– (1)
∠OEB = ∠OFD = 90° ———– (2)
OB = OD ———– (3)
From equations 1, 2 and 3
∆OEB ≅ ∆OFD
BE = FD (By CPCT)
½ AB = ½ CD
Hence, AB = CD
__________________________________________________________________
Theorem 4
“Measures of angles subtended to any point on the circle’s circumference from the same arc are equal to half of the angle subtended at the centre by the same arc.” __________________________________________________________________
[REFERENCE IMAGE ONLY: Using Q instead of D]
In ∆AOP,
∠AOB = 2∠APB
Construction required: Joining PQ passing through the “O”
Poof of the theorem
OA = OP ————— (1)
∠OAP = ∠OPA (Angles opposite to equal sides of triangle) ——————— (2)
∠AOQ = ∠OAP + ∠OPA ——————- (3)
Therefore, from equations 2 and 3
∠AOQ = 2∠OPA ———- (4)
In ∆BOP,
∠BOQ = 2∠OPB ——— (5)
∠AOB = ∠AOQ + ∠BOQ
From equations 4 and 5,
∠AOB = 2∠OPA + 2∠OPB
∠AOP = 2 (∠OPA + ∠OPB)
∠AOB = 2∠APB
Hence proved
__________________________________________________________________
Theorem 5
“The opposite angles in a cyclic quadrilateral are supplementary.”
__________________________________________________________________
[REFERENCE IMAGE ONLY: Using PQRS instead of ABCD]
Proof of the theorem
For arc PQR,
∠POR = 2 ∠PQR = 2α (THEOREM 4) ————— (1)
Considering the arc PSR,
Reflex ∠POR = 2 ∠PSR = 2β (THEOREM 4) —————- (2)
∠POR + Reflex ∠POR = 360°
From equations 1 and 2
2 ∠PQR + 2 ∠PSR = 360°
2α + 2β = 360°
α + β = 180°
__________________________________________________________________
Theorem 6
“Tangent to a circle perpendicular to the radius of the circle at the point of contact”
__________________________________________________________________
[REFERENCE IMAGE ONLY: Using AB instead of PQ]
Here in this diagram,
O is the centre of the circle.
OA ⊥ XY.
__________________________________________________________________
Theorem 7
“Number of tangents can be drawn from a given point.”
__________________________________________________________________
(1) If the point is the circle’s interior region, any line through that particular point will be a secant. Therefore, no tangent can be drawn to a circle that passes through the point that lies inside it.
[REFERENCE IMAGE ONLY]
(2) When the tangency point lies on a circle, there is precisely one tangent to a circle, which passes through it.
[REFERENCE IMAGE ONLY]
(3) When the point is at the circle’s outside, there are precisely two tangents to the circle.
[REFERENCE IMAGE ONLY]
__________________________________________________________________
Theorem 8
“The length of the tangents drawn from any external point is equal.”
__________________________________________________________________
[REFERENCE IMAGE ONLY]
Discover better learning pace and Flexibility
Online tuition by TEL Gurus helps you learn at your own pace and garner the flexibility to choose your preferred timeslots.
Categories
Recent Posts
- List of the qualities you should look for in your tutors?
- What is the most useful formulas in math?
- Describe the process of eating to defecation of food?
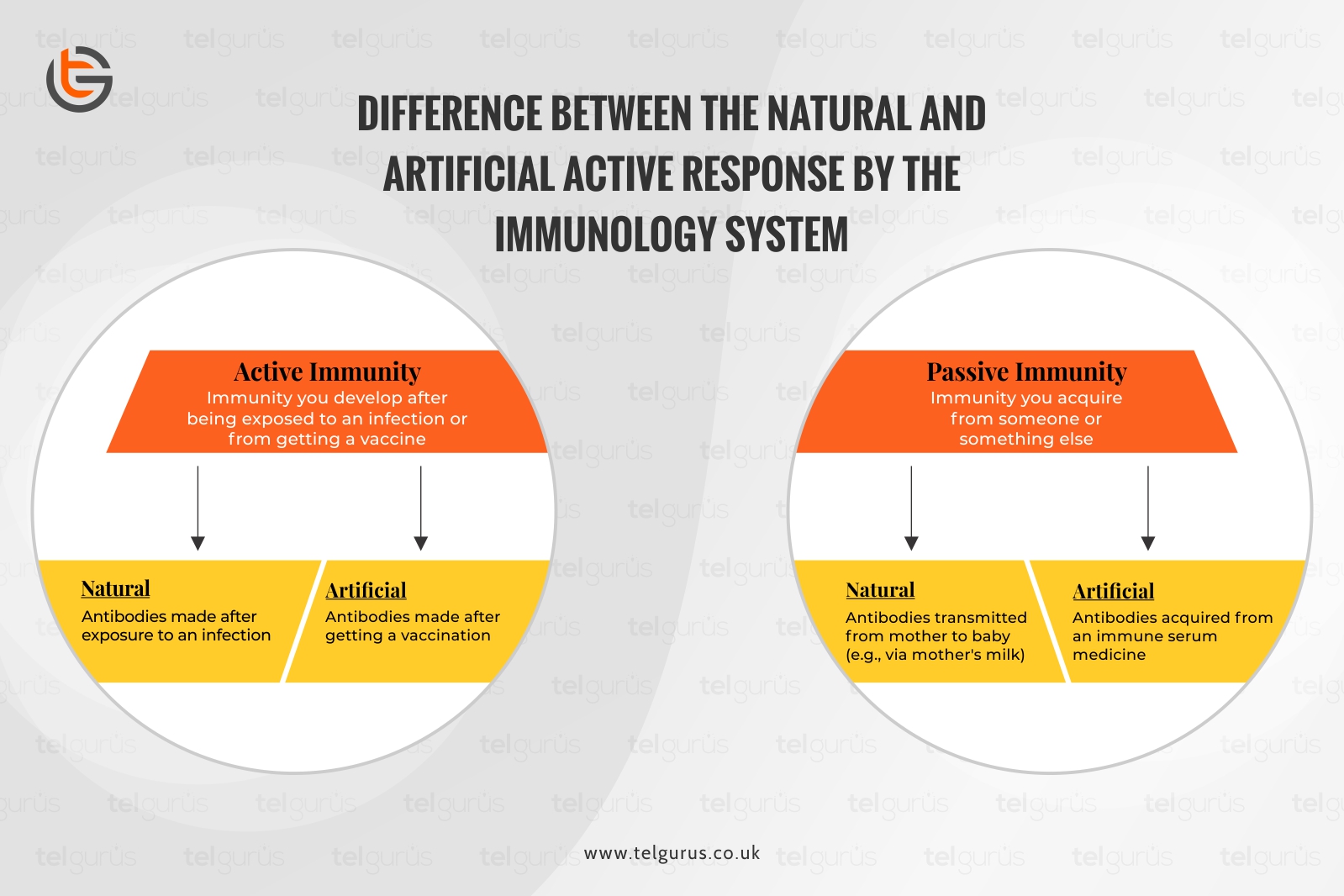
- Difference between the natural and artificial active response by the immunology system.
- Explain the different circle theorems
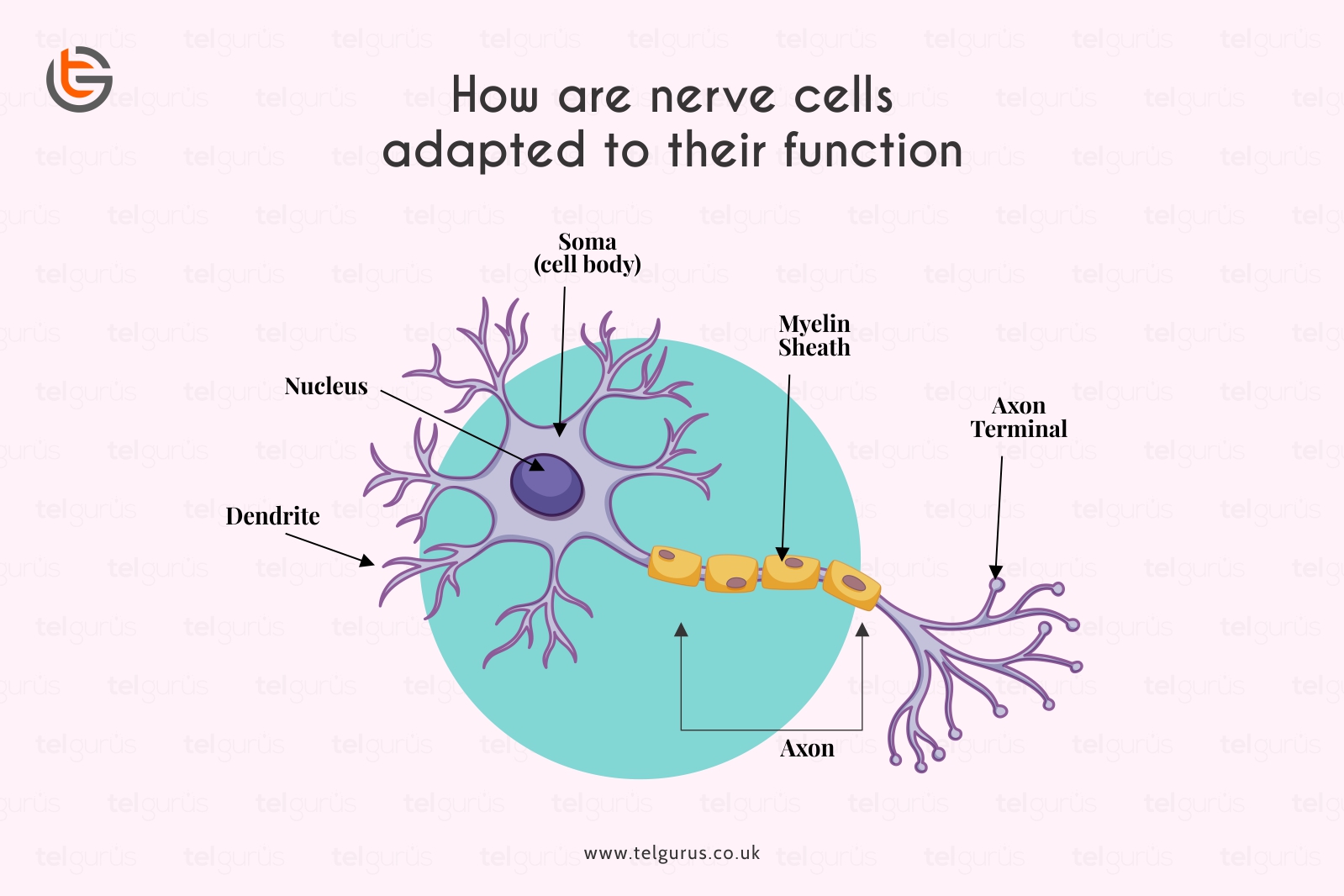
- How are nerve cells adapted to their function?