What is a factor in math?

Book A Demo Class

Factor

Factor is a number that divides a given number completely and gives remainder zero. So, a factor is the divisor of the given number. Also, when we multiply two numbers to find the product, the two numbers that are multiplied are the known as the factors of that product. The factors of a number are the ones that completely divide it into equal parts.

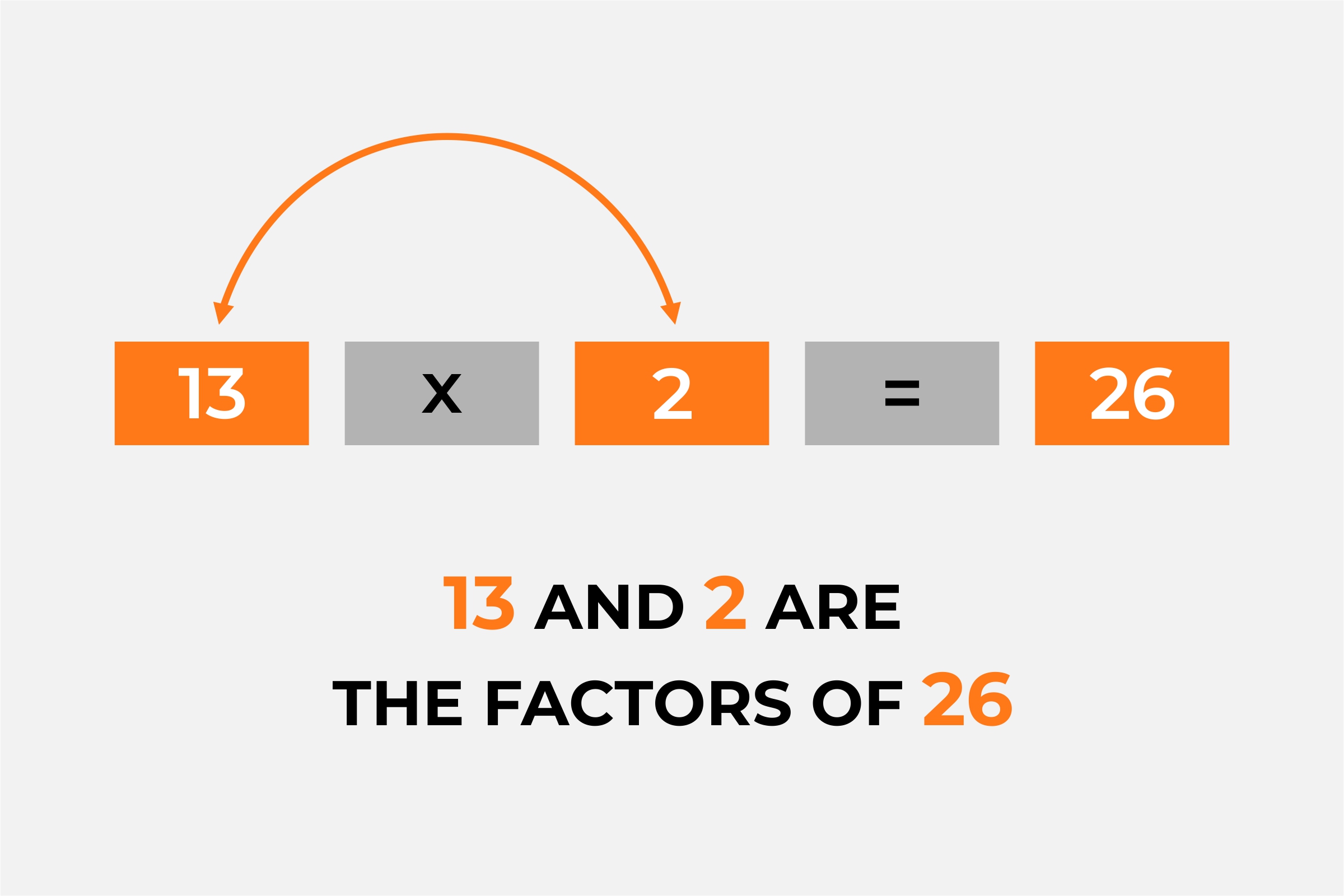
For example:

13 x 2 = 26;

Here 13 and 2 are the factors of 26.

What does the word ‘factor’ means?

Factor is a Latin word that means ‘a performer’, ‘a maker’ or ‘a doer’. The practical applications of factors involve when you aim to divide something into equal parts. Knowledge of factors is also beneficial when you are making calculations while exchanging money, travel or understanding time. Whether it’s arranging essentials in a box or finding patterns, factors are an important part of our everyday lives.

How to find factors of a given number?

To get the factors of a given number, there are two approaches namely multiplication and division.

Method 1: Multiplication

Here you need to find all the combinations where the given number can be expressed as the product of two numbers. All the unique numbers involved (multiplicands and multipliers) are known as the factors of that number.

For example:

Problem: Find out the factors of 18 using multiplication method.

First, we need to find all the combinations where 33 can be expressed as the product of two numbers.

1 x 33 = 33 or, 33 X 1 = 33

11 x 3 = 33 or, 3 x 11 = 33

So, the factors of 33 are 1, 3, 11 and 33.

Method 2: Division

Using division method, list down all the numbers less than or equal to the given number.

Starting from 1, start dividing each number with the given number.
Keep tracking the numbers that give zero as the remainder.
These divisors are the factors. A factor is completely divisible by the given number.

For example:

Problem: Find the factors of 36 using division method.

Here, we need to divide 36 with every number starting from 1 to 36.

So, on dividing with 1, 2, 3, 4, 6, 9, 12, 18 and 36, remainder comes out to be zero.

Hence, these are also known as the factors of 36.

Properties of Factors

There is a finite set of factors for every number.
Except zero and 1, every number has at least two factors, 1 and the number itself.
Factors are always Integers. They are never fractions or decimals.
For all even numbers, 2 is always a factor.
For all numbers ending in 0 and 5, 5 is always a factor.
You can use multiplication and division methods to determine factors.