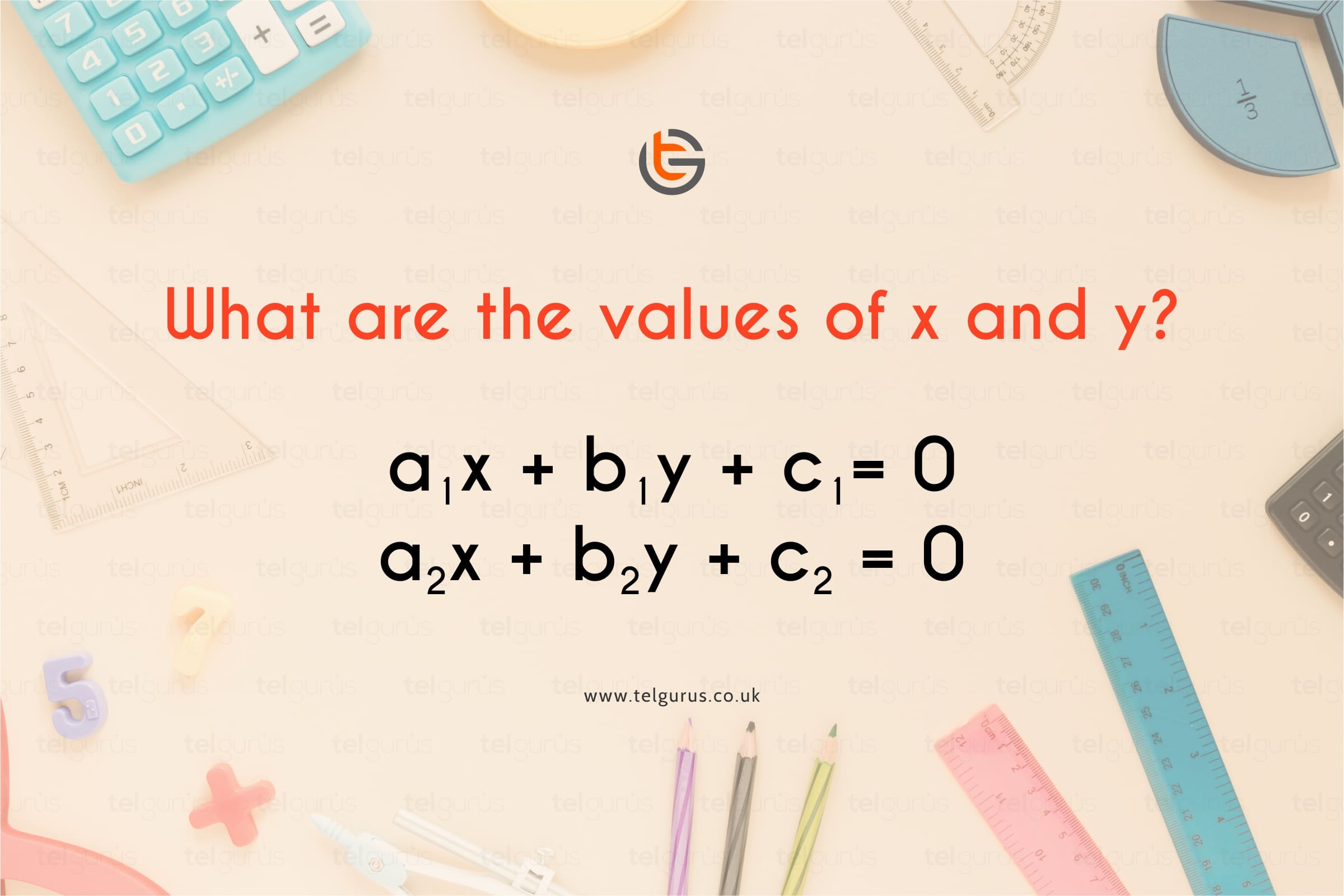Category: Mathematics Questions

The question is indented to solve the equation having two variables x and y. 

 In algebra, an equation can be defined as a mathematical statement which contains an “=” symbol between two algebraic expressions that have same value. 

The most basic and common algebraic equations consist of one or more variables.  

An equation having two variables is called a quadratic equation.  

Let’s discuss how to solve the equation in two variables say x and y. 

The methods to find the values of x and y are  

1). Substitution Method

To understand this method, it’s important to know the steps: 

Step 1 : First of all find the value of one variable , say  y in terms of other variable  that is x from either equation, whichever is convenient  

Step 2: Substitute this value of y in other equation and reduce it to an equation in one variable that is in terms of x which can be solved and we will get the value of x. 

Step 3: Now substitute value of x in the equation used in Step 1 to obtain the value of other variable.  

Take an example to clear this method.  

Example:

Solve the following pair of equations by substitution method: 

\displaystyle ~7x~~-~~15y~~~=~~2                  (1)

\displaystyle ~x~~+~~2y~~~=~~3                  (2)

Step 1: 

Let find the value of x from equation (2) and we get  

\displaystyle ~x~~+~~2y~~~=~~3

\displaystyle ~x~ = ~~3~~~-~~2y                  (3)

Step 2 :  

Substitute the value of x in equation   (1) we get  

7  ( 3 – 2y ) − 15y  =2 

21  −  14y   −  15y  =  2

−29y  = 2 – 21

−29y  =  −19

y  =  19 /  29 

Step 3 : 

 Substitute value of y in equation (3), we get  

 x = 3 − 2 (19 / 29) 

 x = 49 / 29

Therefore the  solution is   

x = 49 / 29 and  y =  19/ 29

2). Elimination Method  

Steps to follow in this method are: 

Step 1:   First step is to make the coefficient of one variable either x or y same in both the equations.  

Step 2: Then add or subtract one equation from the other so that the same variable gets eliminated. Now, we will get the equation in one variable.  

Step 3: Solve the equation in one variable and find out the value. 

Step 4: Substitute this value of x or y in either of the original equations to get the value of the other variable.  

See the example below to clear this method.  

Example :

Solve the following equations by Substitution Method 

 2x  +  3y  =  8                       ( i ) 

4x  +  5y  =  7                        ( ii )  

Sol: Multiply equation (i) by 2 and equation (ii) by 1 to make the coefficients of x equal. Then we get the equations as: 

4x  +  6y  =  16                     (iii)   [on multiplying equation (i) by 2] 

 4x  +  5y  =  7                      (iv)   [on multiplying equation (ii) by 1] 

Subtracting equation (iv) from equation (iii), we get  

 y   =   9 

Put this value of y in either equation (i) or   equation (ii)  

We put value of y in equation (i)  

2x  +  3 ( 9 )  =  8

2x  +  27    =  8

2x  =  8  −  27 

2x   =  − 19

x  =  − 19 / 2  

So , the solution is  

 x  =  − 19 / 2   ,   y   =  9

These are the two methods to solve the equation for   x and   y. 

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Sequence: A sequence is an ordered set of numbers and can either be a finite or an infinite set. 

The two most common types of mathematical sequences are arithmetic sequences and geometric sequences. 

• Arithmetic Sequence  

Arithmetic sequence is that in which difference between two consecutive terms is constant. It is also known as arithmetic progression or AP.  

 Let us clear the concept with an example. 

Let the series be  

{ 5 , 7 , 9 , 11 , 13 , −−−−−−−−−−−−−−− }

Now we can see that in the above example the common difference between two consecutive terms is 2. 

7 – 5 = 2 

9 – 7 = 2

11 – 9 = 2 

13 – 11 = 2

and so on. 

So, the series in which the common difference is same between any two consecutive terms is same is known as arithmetic series.  

In arithmetic series common difference is denoted by d. 

The first term is denoted by a. 

The series become: 

A= a, a + d, a+2d, a+3d, a+4d………

The nth term of an arithmetic progression can be calculated as: 

 𝑨𝒏  = 𝒂 + ( 𝒏 – 𝟏 ) 𝒅 

By putting the values of  a, n and d we can find the arithmetic sequence.  

• Geometric Sequence  

In geometric sequence is created when there is a constant ration between two consecutive terms.  

The two terms differ by a constant multiplier. The sequence obtained is also known as Geometric Progression or GP. 

 If the multiplier is greater than 1, then the terms will get larger with each consecutive term. Here the sequence will be diverging. 

But, on the other hand, if the multiplier is less than 1, then the terms will get start getting smaller. The sequence will be converging in nature.  

In simple terms we can say that unlike arithmetic sequence, in geometric sequence common ratio between any two consecutive terms remains the same.  

Example for Geometric Sequence:

Let the series be  

{ 2 , 6 , 18 ,54 , 162 , ……………..}

We can see in the above example that common ratio between two consecutive terms is same.  

6 / 2 = 3 

18 / 6 = 3 

54 / 18 = 3

So, we can see that here common ratio is same between two consecutive terms that is 3.  

In geometric sequence the common ratio is denoted by the letter ′r′.  

A Geometric Sequence with common ratio  ‘r′ and first term ′a′ can be expressed in the following way.  

The given equation is a quadratic equation which means the power of the variable is 2. It is also known as a polynomial of the second degree.

It is usually written in the form of ax^2 + bx + c =0. Here a, b and c belong to a set of real numbers and where a is never equal to 0 (a ≠ 0). 

For all quadratic equations, there are two values of the variables that satisfy the equation and turn it zero. These are called the roots of the equation. There are two main ways to find the roots of the equation. 

These are  

• Performing factorization 
• Using quadratic formula to find roots.  

Book Your 60-minutes Free Trial class NOW!

Let’s discuss the steps used to solve a quadratic equation. 

Steps to factorize a given equation 

When we say factorize a given quadratic equation, it means breaking the equation into a product of two factors.  

In a nutshell, let’s understand the steps that are followed while factoring a quadratic equation. 

• Expand the expression if needed. 
• Take all terms to the left-hand side of the equal to sign so the right side becomes zero.  

• Arrange all like terms together. Resolve fractions (if any). 
• Break the middle term i.e. the coefficient of the variable with power 1. 

In ax^2 + bx + c = 0, we need to break b into two parts in such a way that on multiplying them you get ac and on adding you get b.  

• Now you have the two factors. Now separate them and equate each of them to zero. 
• You are left with two linear equations that are easy to solve.   

So, let’s start solving the equation x^2 + 5x + 6 = 0 

Here, a  = 1, b = 5 and c = 6; 

ac = 6 and b = 5 

Here, we need to break 5 into two parts in such a way that it gives 6 ( a*c = 1* 6 = 6 ) on multiplication and the addition should be 5 (b). 

So, the two values are 2 and 3 which in addition give 5 and on multiplication give 6. 

x^2 + 5x + 6  can be written as x^2 +  3x + 2x + 6 

Here, comes the splitting part. Taking out x (common) thing from the first two terms and taking 2 common factors from the last two terms.  

x^2 + 5x + 6 = x ( x + 3) + 2 (x + 3)  

Taking aside (x + 3), we get two linear equations. 

It becomes: 

(x + 2) (x + 3) = 0 

Now we have got two linear equations (x + 2) and (x + 3). 

Equate them to zero individually. 

x + 2 = 0 and x + 3 = 0 

This makes, x = -2 and x = -3 

So, the roots or zeros of x^2 + 5x + 6 equation are -2 and -3. 

Another method is by using a quadratic formula: 

The roots of any equation can be solved by using the following formula 

x=\frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}

First root,   x=\frac{{-b+\sqrt{{{{b}^{2}}-4ac}}}}{{2a}} and the second root is   x=\frac{{-b-\sqrt{{{{b}^{2}}-4ac}}}}{{2a}}

By putting the values of a, b and c  

We get, the first root as  

x=\frac{{-5~+~\sqrt[{}]{{{{5}^{2}}-4*6}}}}{{2*1}}

x =( -5 + √1)  / 2 

x = -4 / 2  

x =  -2 

We get the second root as: 

x=\frac{{-5~-~\sqrt[{}]{{{{5}^{2}}-4*6}}}}{{2*1}}

x =( -5 – √1)  / 2 

x = -6 / 2  

x =  -3 

So, by using the quadratic formula we get the roots of x^2 + 5x + 6 as -2 and -3. 

Book Your 60-minutes Free Trial class NOW!

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Just like their literal meaning, maxima and minima in mathematics mean finding the maximum and the minimum values of a function within a given domain.   

Let’s check a few practical applications of the importance of maxima and minima function. 

• To an engineer, these maximum and minimum values of a function helps in determining real life values of a function and help them analyze the practical scenarios and implementation part.  
• To an economist, the maximum and minimum values of the total profit function helps to decide the salaries and other expenses of the company so as to keep the budget in control and avoid loss.  
• To a doctor the maximum and minimum values of the function help determine the right prescription for the patient.  

For example: Values for glucose/sugar levels in the bloodstream are used to determine the dosage the doctor needs to prescribe to different patients to bring their blood glucose levels to normal.  

Maxima and minima are respectively the highest and lowest point on the curve.  

Let’s discuss how to find the maxima and minima of a function.  

Methods to find maxima and minima of a function  

Maxima and minima of a function can be calculated by using the first – order derivative test and second – order   derivative test.  

These are the quickest ways to find the maxima and minima.  

First order derivative test for Maxima and Minima

The first derivative of any function gives you the slope of the function.  

Near a maximum point, the slope of the curve increases as we go towards the maximum point then becomes zero at the maximum point and then decreases as we move away from the maximum point. 

Similarly, is in the case of minima.  

Let say we have a function  f  which is  continuous at the critical point, defined in an open interval  and  f’ ( c )  =  0. 

Then we check the value of f’( x )  at the point left to the curve and right to the curve and check the nature of  f’( x ), then we can say that the given point will  be: 

# Local maxima : If f’ ( x )  changes sign from positive to negative as x increases via point c,  then  f ( c )  gives the maximum  value of the function  in that range.  

# Local minima :  If f’ ( x )  changes sign from  negative to positive as x increases via point c , then f ( c ) gives the minimum value of the function in that range .  

# Point of inflection :  If the sign of f’( x )  doesn`t change  as  x increases via c, and point c is neither the maxima nor the minima of the function , the point c is called the point of inflection.  

 Second order derivative Test for Maxima and Minima

 In the second order derivative test for maxima and minima, we find the  first order derivative of the function and if it gives the value  of the slope equal to zero  at the critical point x = c [( f’ ( c )  = 0 ] , then we find the second derivative of the function. If the second order derivative of the function exists within the given range, then the given point will be:  

# Local maxima:  If  f’’ ( c )  ˂ 0  

# Local minima:  If  f’’ ( c )  ˃ 0  

# Test fails:  If f’’ ( c )  =  0  

So, by these two methods we can find the maxima and minima of a function.  

 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Before proceeding forward, let’s understand the meaning of profit maximization. 

What is profit maximization?  

The process by which different enterprises make strategies to make high profits with lower expenditure is called profit maximization. 

It is a basic target of every business or firm and is vital for its progress. The expenditure of a firm that goes into the manufacturing and delivery of products is known as its Total Cost of Production (TC). 

 The income of a firm coming from the sale of its products/ services is called Total Revenue (TR). 

The difference between the Total Cost of production (TC) and Total Revenue (TR) constitutes the profit of the company or the enterprise. The profit is denoted by the symbol π or pi.  

Therefore,   π = TR – TC  

This means that profit is equal to the difference between the total revenue and total cost.  

In order to achieve maximum profits, it has to reach a stage of equilibrium. 

What is equilibrium?

 A firm is said to be in equilibrium position when its level of output give rise to maximum difference between total revenue and total cost, and it has no intention to change its existing level of production. 

 There are two methods of determining profit maximization in perfect competition which are mentioned below: 

Methods of Determining Profit Maximization: 

1). Comparing Total Cost and Total Revenue

Total profits of a firm are found my calculating the difference between total revenues and total costs.  

Total profits will keep increasing as long as the change in total revenue continues to surpass or exceed the change in total cost of production. 

In this scenario, for a perfect competition firms need to figure out the exact quantity of commodities that need to be sold in order to earn more profits.  

2).  Comparison Between Marginal Revenue and Marginal cost 

Another method of determining maximum profit is the MC MR approach. 

The change in Total Cost of Production (TC) incurred with the manufacturing of an additional unit is known as Marginal Cost (MC. 

MC can be represented mathematically as: 

 MC = Change in total cost / Change in quantity  

Similarly, the change in Total revenue resulting from the sale of an additional unit is known as Marginal Revenue or MR.  It can be represented as:  

MR = Change in total revenue / Change in quantity  

Every time there is a demand for an additional unit that company products meets, the revenue increases by an exact  amount equal to prevailing market price.   

Why is profit maximised when MR = MC?

At production levels of MR = MC, the difference between the total revenue and total cost is maximum which serves as our requirement for producer’s equilibrium and leads to profit maximization. 

However, profits begin to fall again when MC  ˃ MR 

Therefore, MC ˂ MR is a necessary condition for sustainable profit scenario. 

The firm needs to take into account what happens when it changes its production by one unit, if aiming to maximize the profits.  

The firm will incur extra production costs even for producing one single unit, but will also receive revenue from that unit. 

If the MC is bigger than MR obtained, the firm should realize that producing an extra unit was not profitable at all.  

The firm should continue the production till MC = MR because producing an extra unit beyond this point will not be profitable for the firm.  

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

The key to tell the difference between LCM and HCF is to know the difference between a multiple and a factor. 

What is a multiple?

A multiple of a number is any number that appears in its times table.  

For example, the multiples of 3 are 3, 6, 9, 12 and so on.  

What is a factor? 

A factor of a number is any integer that divides that number without leaving any remainder. 

For example factors of 9 are 1, 3 and 9. 

To know the difference between HCF and LCM of two numbers we must know the meaning of HCF and LCM first. 

HCF

HCF is defined as the Highest Common Factor of two or more given numbers. 

It is also called Greatest Common Divisor (GCD). 

For example: 

The HCF of 36 and 24 is 12, because 12 is the largest number that divides both the numbers completely without leaving any remainder.  

LCM 

LCM is the Least Common Multiple of two or more numbers. It turns out to be the smallest number that is a common multiple of the given numbers.  

Example: Let us take two numbers 16 and 8  

Multiples of 16 are:  16, 32, 48, 64, 80, 96 and so on.  

Multiples of 8 are : 8 , 16 , 24 , 32 , 40  , 48 , 56 , 64 and so on .  

We can see from above that the first common value among these multiples is 16. 

 Therefore, 16 is the LCM or least common multiple of the two numbers 16 and 8.  

Now this was about the meaning of HCF and LCM.  

From the above discussion we can conclude that LCM and HCF are two entirely different concepts with following differences: 

Differences between HCF and LCM

1). Definition

 The main difference between HCF and LCM lies in their definitions.  

While HCF is all about calculating the highest number that divides a given number into two or more equal parts, LCM means finding a common multiple of the lowest value shared by the given numbers.  

2).  Full Form  

HCF stands for Highest common factor for two or more given numbers. LCM is the abbreviation used for the Least Common Multiple for two or more numbers.  

3). Type

The LCM number is generally a composite number when calculated correctly. Whereas the HCF can either be a prime number or composite number depending on the given numbers.  

While HCF is the largest real number shared by all the given numbers, LCM is the smallest number that can be divided by the given numbers.  

4). Other names

HCF is also as GCF or GCD while LCM is more or less the only term used to convey the least multiple which is common to a given set of numbers.  

5). Calculations

The methods of finding both LCM and HCF are different from each other.  Though it says “least” common multiple, the answer is always greater than the numbers.  

Similarly, for HCF. It says “Highest” common factor, the answer is always lowest from all the three numbers.  

For example: 

Find the LCM and HCF of 10, 15 and 20. 

For LCM, Let’s use the ladder method 

2	10, 15, 20
2	5, 15, 10
3	5, 15, 5
5	5, 5, 5
	1, 1, 1

LCM of 10, 15 and 20 is 2 * 2* 3 * 5 = 60 

For HCF, we need to calculate the factors and then find the common amongst them. 

Factors of 10: 1, 2, 5, 10 

Factors of 15: 1, 3, 5, 15 

Factors of 20: 1, 2, 4, 5, 10, 20 

The common factors are 1 and 5, out of which 5 is the biggest number.  This means 5 is the HCF of 10, 15 and 20.  

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development