Enrich your knowledge with our informative blogs
What are the values of x and y?
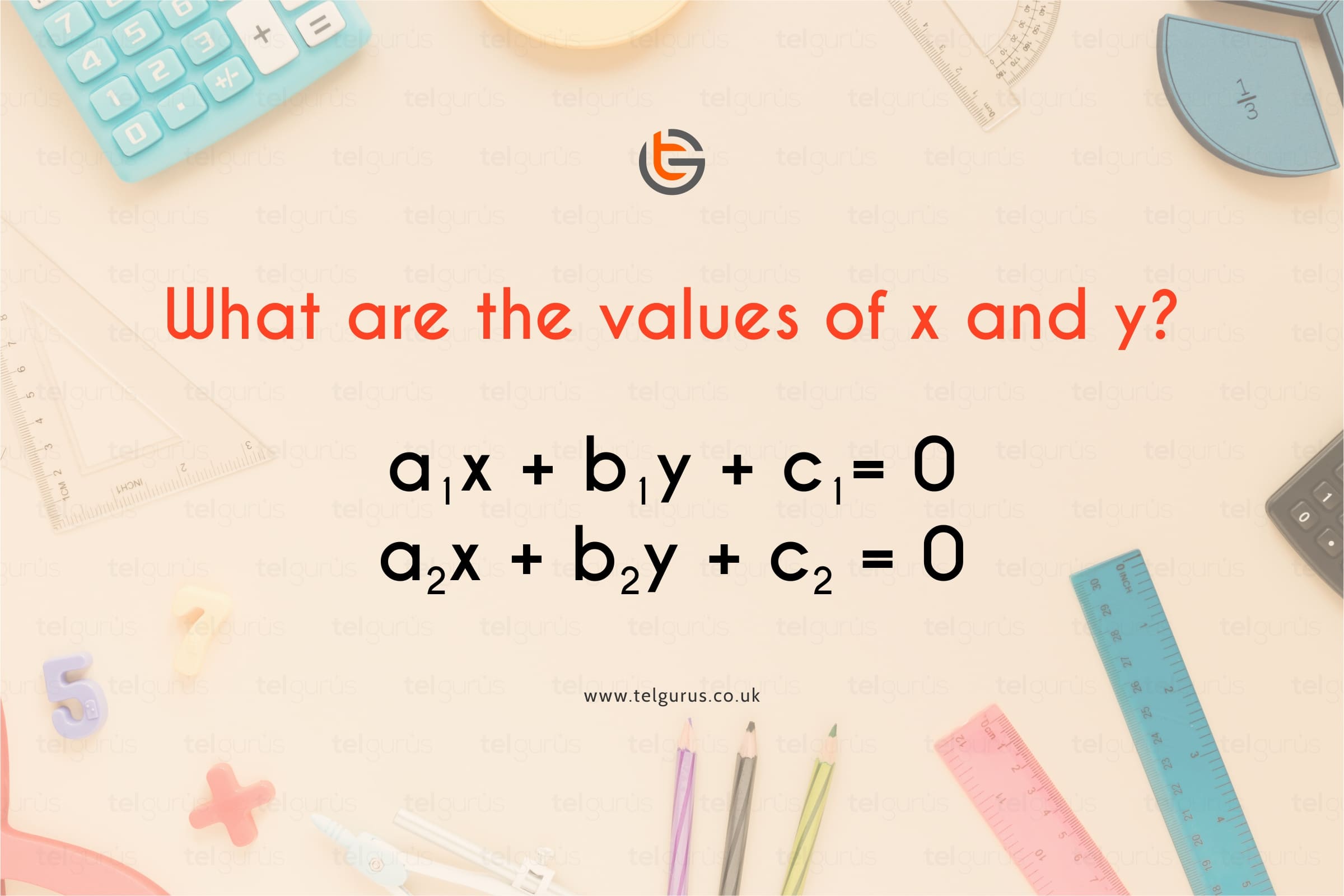
The question is indented to solve the equation having two variables x and y.
In algebra, an equation can be defined as a mathematical statement which contains an “=” symbol between two algebraic expressions that have same value.
The most basic and common algebraic equations consist of one or more variables.
An equation having two variables is called a quadratic equation.
Let’s discuss how to solve the equation in two variables say x and y.
The methods to find the values of x and y are
1). Substitution Method
To understand this method, it’s important to know the steps:
Step 1 : First of all find the value of one variable , say y in terms of other variable that is x from either equation, whichever is convenient
Step 2: Substitute this value of y in other equation and reduce it to an equation in one variable that is in terms of x which can be solved and we will get the value of x.
Step 3: Now substitute value of x in the equation used in Step 1 to obtain the value of other variable.
Take an example to clear this method.
Example:
Solve the following pair of equations by substitution method:
\displaystyle ~7x~~-~~15y~~~=~~2 (1)
\displaystyle ~x~~+~~2y~~~=~~3 (2)
Step 1:
Let find the value of x from equation (2) and we get
\displaystyle ~x~~+~~2y~~~=~~3\displaystyle ~x~ = ~~3~~~-~~2y (3)
Step 2 :
Substitute the value of x in equation (1) we get
7 ( 3 – 2y ) − 15y =2
21 − 14y − 15y = 2
−29y = 2 – 21
−29y = −19
y = 19 / 29
Step 3 :
Substitute value of y in equation (3), we get
x = 3 − 2 (19 / 29)
x = 49 / 29
Therefore the solution is
x = 49 / 29 and y = 19/ 29
2). Elimination Method
Steps to follow in this method are:
Step 1: First step is to make the coefficient of one variable either x or y same in both the equations.
Step 2: Then add or subtract one equation from the other so that the same variable gets eliminated. Now, we will get the equation in one variable.
Step 3: Solve the equation in one variable and find out the value.
Step 4: Substitute this value of x or y in either of the original equations to get the value of the other variable.
See the example below to clear this method.
Example :
Solve the following equations by Substitution Method
2x + 3y = 8 ( i )
4x + 5y = 7 ( ii )
Sol: Multiply equation (i) by 2 and equation (ii) by 1 to make the coefficients of x equal. Then we get the equations as:
4x + 6y = 16 (iii) [on multiplying equation (i) by 2]
4x + 5y = 7 (iv) [on multiplying equation (ii) by 1]
Subtracting equation (iv) from equation (iii), we get
y = 9
Put this value of y in either equation (i) or equation (ii)
We put value of y in equation (i)
2x + 3 ( 9 ) = 8
2x + 27 = 8
2x = 8 − 27
2x = − 19
x = − 19 / 2
So , the solution is
x = − 19 / 2 , y = 9
These are the two methods to solve the equation for x and y.
Read More – Mathematics Questions
View More – Useful links for Your Child’s Development

Unleash the Power of visualization to break tough concepts
Wanna be the next Maths wizard? Discover the new way of learning concepts with real-life Visualization techniques and instant doubt resolutions.
Categories
Recent Posts
- List of the qualities you should look for in your tutors?
- What is the most useful formulas in math?
- Describe the process of eating to defecation of food?
- Difference between the natural and artificial active response by the immunology system.
- Explain the different circle theorems
- How are nerve cells adapted to their function?