Simplify and then solve by factorization 3x ( x + 2 ) – 7 = 2 , to find x.

Book A Demo Class

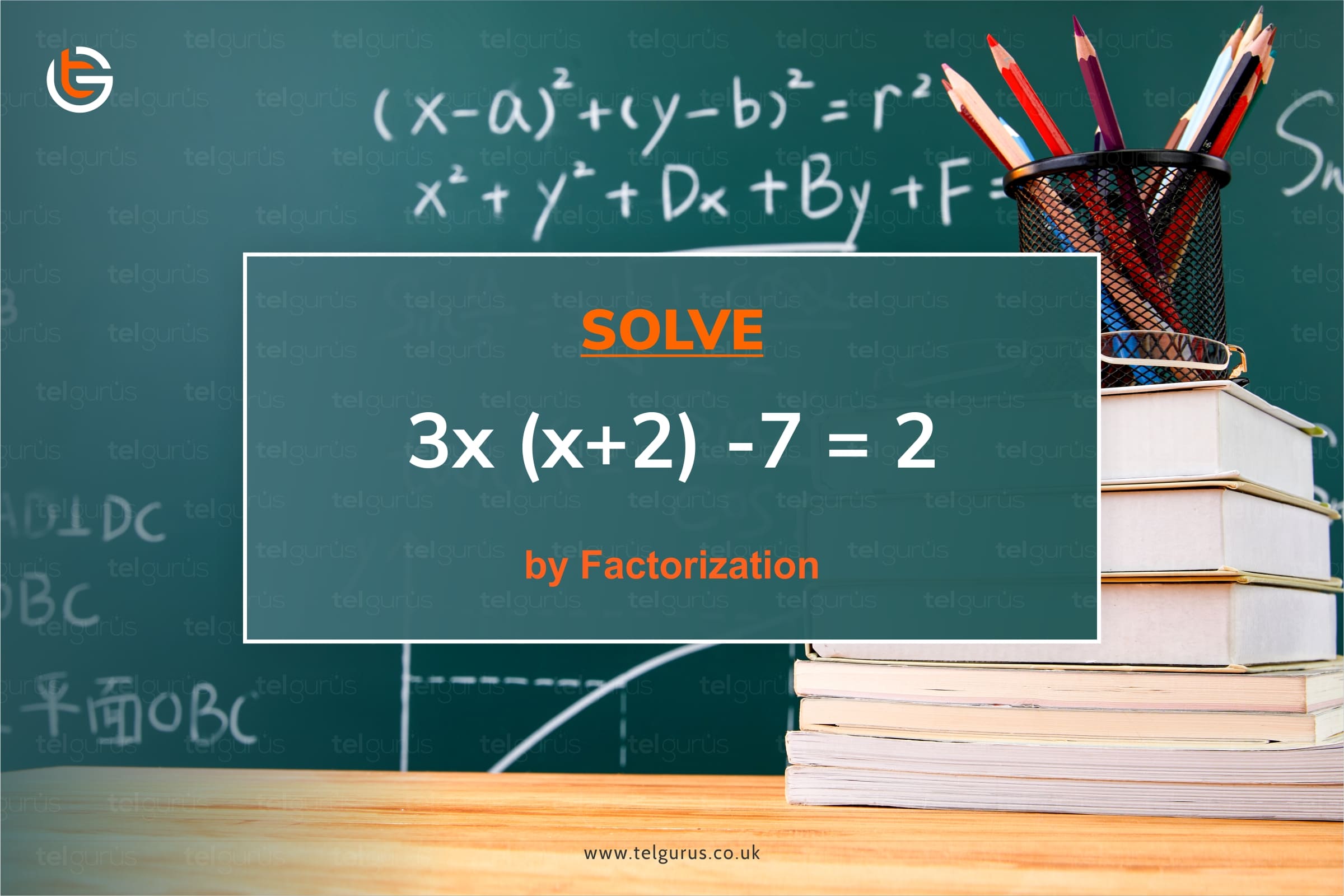
In the question what we have to solve is the equation. In algebra, an equation can be defined as a mathematical statement which contains an equal symbol between two algebraic expressions that have same value.

In mathematics, the most basic and common algebraic equations consist of one or more variables.

For Example:

3 x + 5 = 14 is an equation , in which 3 x + 5 and 14 are two expressions separated by an “ = “ sign.

Equation means, expression on the left hand side is always equal to the right hand side.

An equation consists of variables and constants. $a, b, c, x, y$ etc are known as variables where as numbers like $2, 5, 9$ are constants. The process of finding the value of the variable is called solving the equation. There are different types of equation in mathematics.

Equations are of many types like linear, quadratic, trigonometric, radical, polynomial, exponential equations etc.

Equation where the power of variable is 2 is called a quadratic equation.

The equation given in the question is the quadratic equation as there are two $x$ ’s. We have to solve by the method of factorization. And for that we have to follow the following steps:

- Convert the quadratic equation into standard form that is $\displaystyle a{{x}^{2}}~+~bx~+~c~=~0$
- Multiply the coefficient of $\displaystyle {{x}^{2}}~$ (a) and the constant term (c), we get ac.
- Now try to find two numbers whose product is ac and whose sum or difference is equal to b that is the coefficient of x.
- Factorize the given expression on Left hand side with zero on right hand side.
- Equate each factor equal to zero.
- In this way we get the required two roots of the equation.

Now, we have been given the equation $3 x (x + 2) - 7 = 2$ .

Before applying the above rules of factorization we will first simplify the equation.

$3 x (x + 2) - 7 = 2$

First we will multiply $3 x$ by the whole bracket. And we get :

$\displaystyle 3{{x}^{2}}~+~6x~-~7~=~2$

$\displaystyle 3{{x}^{2}}~+~6x~-~7~-~2~=~0$ $3 x^{2} + 6 x - 7 - 2 = 0$

After simplification, we get

$\displaystyle 3{{x}^{2}}~+~6x~-~9~=~0$

Now we will apply above steps of factorization to find the value of $x$ .

At first we will multiply the coefficient of $\displaystyle {{x}^{2}}~$ and the constant term. In the given equation coefficient of $\displaystyle {{x}^{2}}~$ is $3$ and the constant term is $- 9$ and by multiplying both of them we get $(- 27) .$

Now, we have to find the two numbers whose product is ( – 27 ) and by subtracting or adding those numbers we get the coefficient of $x$ that is ( +6 ). And the two numbers are (+9) and (- 3 ) that give +6 on addition and -27 on multiplying.

Now,

$\displaystyle 3{{x}^{2}}~+~6x~-~9~=~0$

$\displaystyle 3{{x}^{2}}~+~9x~-~3x~-~9~=~0$ $3 x^{2} + 6 x - 7 - 2 = 0$

$3 x (x + 3) - 3 (x + 3) = 0$

$(3 x - 3) (x + 3) = 0$

That means either

$3 x - 3$ = 0 or $x + 3$ = 0

Solving these we get

x = 1 or x = − 3

So, 1 and – 3 are the two values of x for the given equation.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development