How do you find the square roots of a complex number?

• Book A Demo Class

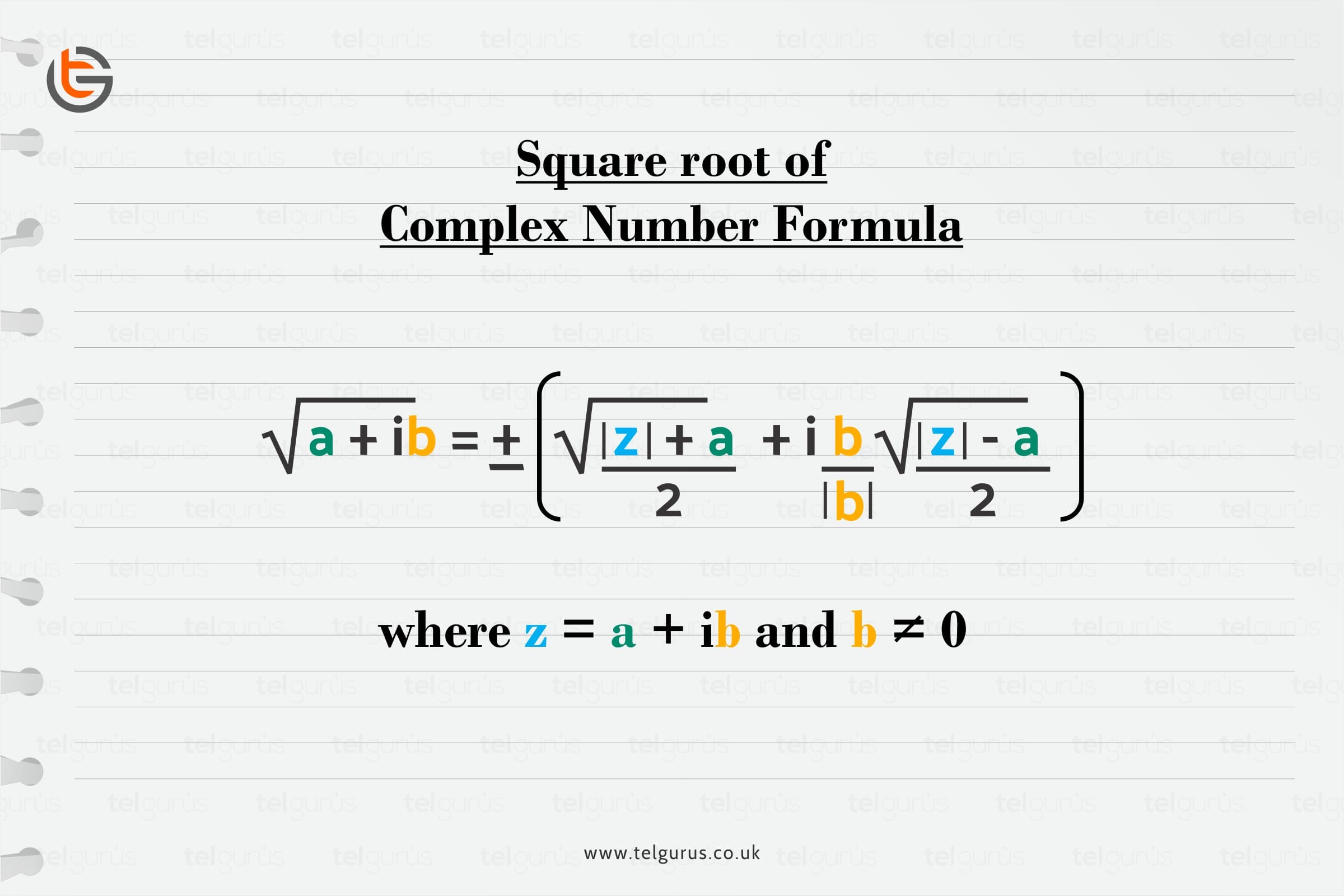
Before finding the square root of a complex number we must know what complex numbers are.  

A complex number is the sum of a real number and an imaginary number.  

It is written generally in the form of a + ib and it is represented by alphabet z.  

Here, both a and b are real numbers.  The value ‘a’ is called the real part and is denoted by Re ( z ). 

The imaginary part is denoted by b and is represented as  Im ( z ).  

The alphabet ‘i’ is known as iota and represents the imaginary part of the complex number.  

Further iota is very helpful to find the square root of negative numbers. 

• \displaystyle i=\sqrt{{-1}}~~
• \displaystyle {{i}^{2}}=~-1~~
• \displaystyle {{i}^{3}}=i.{{i}^{2}}\Rightarrow i(~-1)=-i~~

And so on. 

The modulus of the complex number is the distance of the complex number represented as a point in the plane (a, ib). 

Here are some important points regarding complex numbers. 

• All real numbers are complex numbers but the vice versa is not true.  
• All imaginary numbers are complex numbers but vice versa needn’t need to be true. 
• The conjugate of a complex number  z  = a  +  ib   is  z  =  a   –  ib 

• The magnitude of a complex number z = a + ib  is  | z |  = \displaystyle \sqrt{{{{a}^{2}}+{{b}^{2}}}}~~

Now, let’s discuss how can we find the square root of a complex number? 

So, given below are some steps which we have to follow to find the square root of a complex number.  

Firstly , suppose   x + iy  be the square root of the complex number  a  +  ib .  Then we can say, 

 x + iy  = √ ( a + ib) 

as we have supposed  x + iy be the square root of  a + ib 

 Now squaring both sides we get , 

Putting the value of  \displaystyle {{i}^{2}}=-1

\displaystyle {{x}^{2}}-{{y}^{2}}+i(2xy)=a+ib

Now, equating real and imaginary parts, we get: 

\displaystyle {{x}^{2}}-{{y}^{2}}=a   and    2xy =  b   

Now    \displaystyle {{({{x}^{2}}+{{y}^{2}})}^{2}}={{({{x}^{2}}-{{y}^{2}})}^{2}}+4{{x}^{2}}{{y}^{2}}

                                      = \displaystyle {{a}^{2}}+{{b}^{2}}

Now we have  \displaystyle ({{x}^{2}}+{{y}^{2}})=\sqrt{{({{a}^{2}}+{{b}^{2}})}} ……………….  ( 1 )  

Also ,   \displaystyle {{x}^{2}}-{{y}^{2}}=a   ………………………………. ( 2 ) 

Adding equation (  1 ) and equation ( 2 ) we get ,  

\displaystyle {{x}^{2}}=1/2(\sqrt{{({{a}^{2}}+{{b}^{2}}}})+a)=h ( say )  

Now , subtracting equation  ( 2 )  from  equation ( 1 )  we get ,  

\displaystyle {{y}^{2}}=1/2(\sqrt{{({{a}^{2}}+{{b}^{2}}}})-a)=k ( say )  

Thus, 

x  = √ h , – √ h  and  y  =  √ k , – √ k  

In this way we can find the square roots of a complex number. 

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Unleash the Power of visualization to break tough concepts

Wanna be the next Maths wizard? Discover the new way of learning concepts with real-life Visualization techniques and instant doubt resolutions.

Book A Demo Class

• 

  How do you know how many roots a quadratic equation has?

• 

  How is trigonometry used on non-right angled triangles?