Enrich your knowledge with our informative blogs
How to find the acute angle between two intersecting lines whose equations are in vector form?
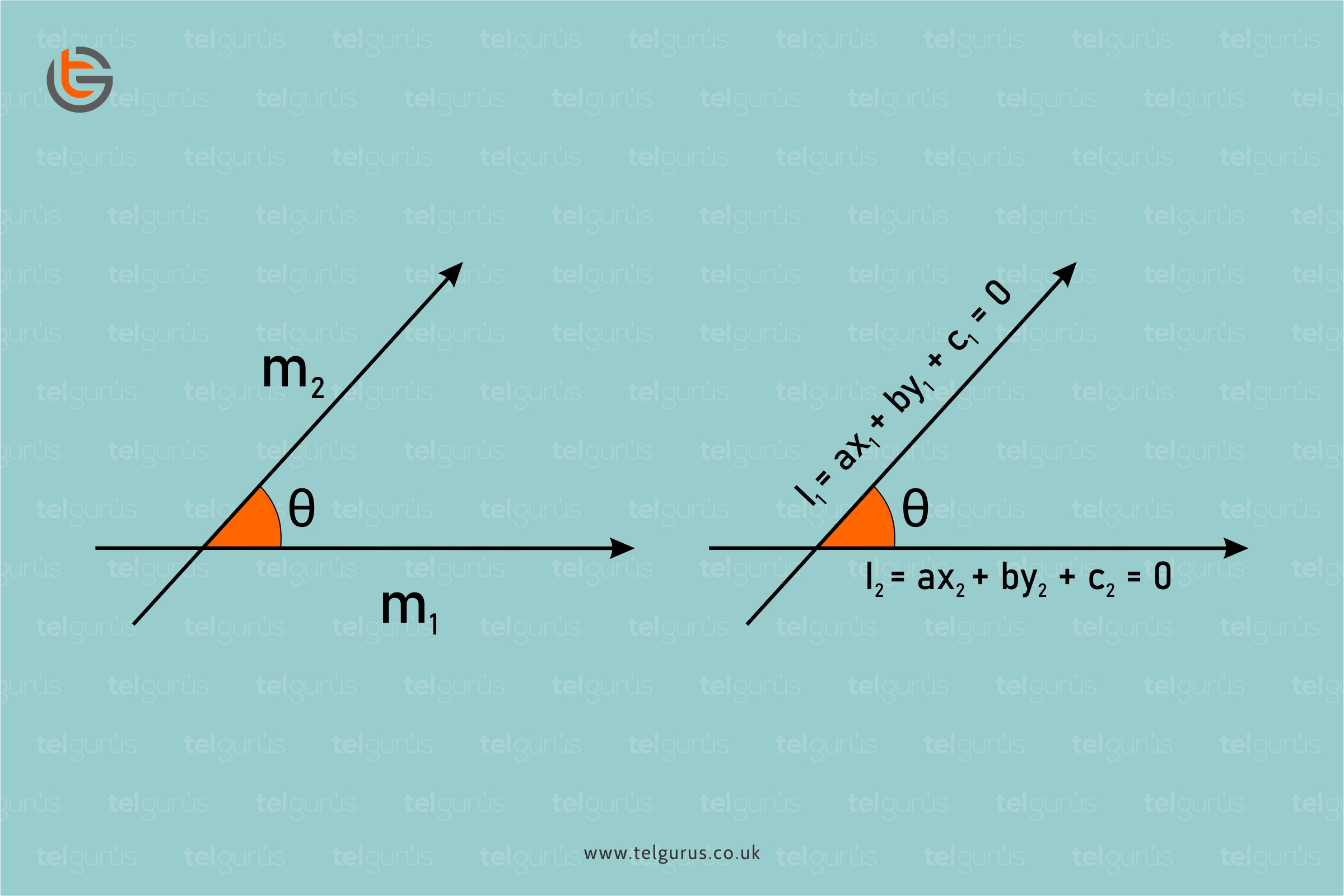
In mathematics, a vector quantity is that which has magnitude as well as direction. When two straight lines intersect, they form two sets of angles.
The intersection forms a pair of acute and another pair of obtuse angles. If the intersecting lines are perpendicular to each other than the angle between them is 90°.
But if they are not perpendicular and are forming acute angle then, there is a special formula to find the acute angle between the two intersecting lines.
Let θ be the angle between the vectors. Therefore the required formula is:
||u|| & ||v|| means the length of vectors u and v.
u.v is the scalar product or dot product of the two vectors.
Let us clear the concept with an example:
Let the two dimensional vector
u = ( 2 , 2 ) and vector v = ( 0 , 3 ).
These can be written as
u = 2 i + 2j and v = 0i + 3j
This is an example of two dimensional vectors but the method can be applied for vectors with any number of components.
Now our first step is to calculate the length of each vector. We can calculate it in the following way
ǀǀuǀǀ = \displaystyle \sqrt[{}]{{\text{u}_{\text{i}}^{2}+~\text{u}_{\text{j}}^{2}}}
= \displaystyle \sqrt[{}]{{{{2}^{2}}+~{{2}^{2}}}}
= \displaystyle \sqrt[{}]{{4+4}}
= \displaystyle \sqrt[{}]{8}
= \displaystyle 2\surd 2
Similarly,
ǀǀvǀǀ = \displaystyle \sqrt[{}]{{\text{v}_{\text{i}}^{2}+~\text{v}_{\text{j}}^{2}}}
= \displaystyle \sqrt[{}]{{{{0}^{2}}+~{{3}^{2}}}}
= \displaystyle \sqrt[{}]{{0+9}}
= \displaystyle \sqrt[{}]{9} = 3
If the vector has more than two components simply continue adding in the same way.
Now it’s the time to find the scalar product of both the vectors .
It is also known as dot product or scalar of the vectors.
To calculate the dot product in terms of the vector’s component, multiply the components in each direction together and then add all the results.
Dot product of both vectors = ui vi + uj vj
Now values of ui, vi, uj and vj are 2, 0, 2 and 3 respectively.
By putting all these values in the above mentioned formula we get :
Dot product of both vectors = ( 2 ) ( 0 ) + ( 2 ) ( 3 )
= 0 + 6 = 6
So, 6 is the dot product of both vectors.
Now by substituting all the values of length of vectors and their dot product in above mentioned equation relating to angle, we get:
\displaystyle \cos \theta =\frac{{u.v}}{{\left\| u \right\|.\left\| v \right\|}}\displaystyle \cos \theta ~=~\frac{6}{{2\sqrt[{}]{2}~.~~3}}
\displaystyle \cos \theta ~=~\frac{6}{{6\sqrt[{}]{2}~}}
\displaystyle \cos \theta ~=~\frac{1}{{\sqrt[{}]{2}~}}
\displaystyle \theta =co{{s}^{{-1}}}\left( {\frac{1}{{\sqrt[{}]{2}}}} \right)
\displaystyle \theta =45{}^\circ
This means the acute angle between these two given interesting lines is 45°.
How do we know two lines intersect each other?
For two lines to intersect, there must a point where they meet. This means that the co-ordinates of x,y,z of one line must be equal to x,y,z of the other line at some point. We are assuming a 3-D plane here.
Let’s understand this by an example:
There are two lines,
L1: x = 2t +2, y = t-1 , z= t+1
L2: x = s-1, y = -s -1, z= 2s -2
Before finding the angle between the lines, you need to prove that these two lines intersect.
For these lines to intersect there must be a point where L1(x,y,z) = L2(x,y,z).
By equating the coordinates of x, y and z, we get three equations:
2t + 2 = s -1 => 2t –s = -3 (i)
t -1 = -s -1 => t + s = 0 (ii)
t + 1 = 2s -2 => t -2s = -3 (iii)
by solving equation (i) and (ii), we get
3t = -3
t = -1
Substituting the value of t in (ii), we get s = 1
x = 0, y = -2, z = 0
So, we get the coordinates where two lines intersect as (0,-2, 0).
Now, we know that the lines intersect; we can easily find the angle between them.
Read More – Mathematics Questions
View More – Useful links for Your Child’s Development

Unleash the Power of visualization to break tough concepts
Wanna be the next Maths wizard? Discover the new way of learning concepts with real-life Visualization techniques and instant doubt resolutions.
Categories
Recent Posts
- List of the qualities you should look for in your tutors?
- What is the most useful formulas in math?
- Describe the process of eating to defecation of food?
- Difference between the natural and artificial active response by the immunology system.
- Explain the different circle theorems
- How are nerve cells adapted to their function?