How to remember the values of sin 60 , sin 30 , sin 45 , etc . ?

Book A Demo Class

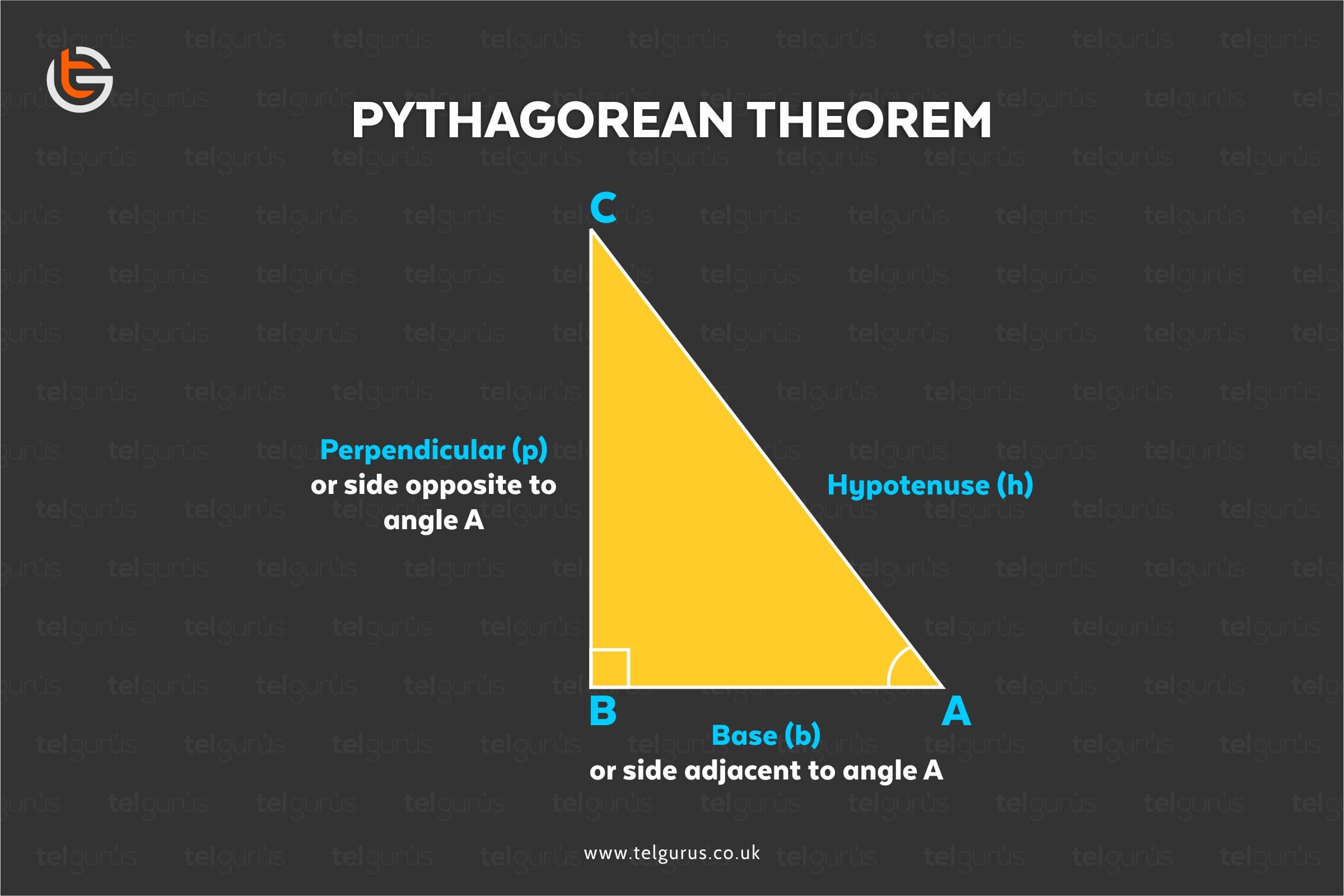
Trigonometry has three most important functions which are primarily used by the students to find out the unknown value of an angle and the length of sides of a right angled triangle. The names and abbreviations of these three functions are sine (sin), cosine (cos) and Tangent (tan).

These three are the primary functions and there are other three trigonometric functions which are the reciprocals of these functions.

Cosecant (cosec) is the reciprocal of sine, Secant (sec) is the reciprocal of cosine and Cotangent (cot) is the reciprocal of tangent.

The values of these functions are used in trigonometric equations.

But the question is how to remember the values of these functions.

There is a table of the values of the trigonometric functions but remembering all the values from the table is a daunting task.

First we will discuss the simple method by means of which we can calculate the value of sine ratios for all the degrees.

With this method, you can easily calculate the values for all other trigonometry ratios.

Read More – Mathematics Questions

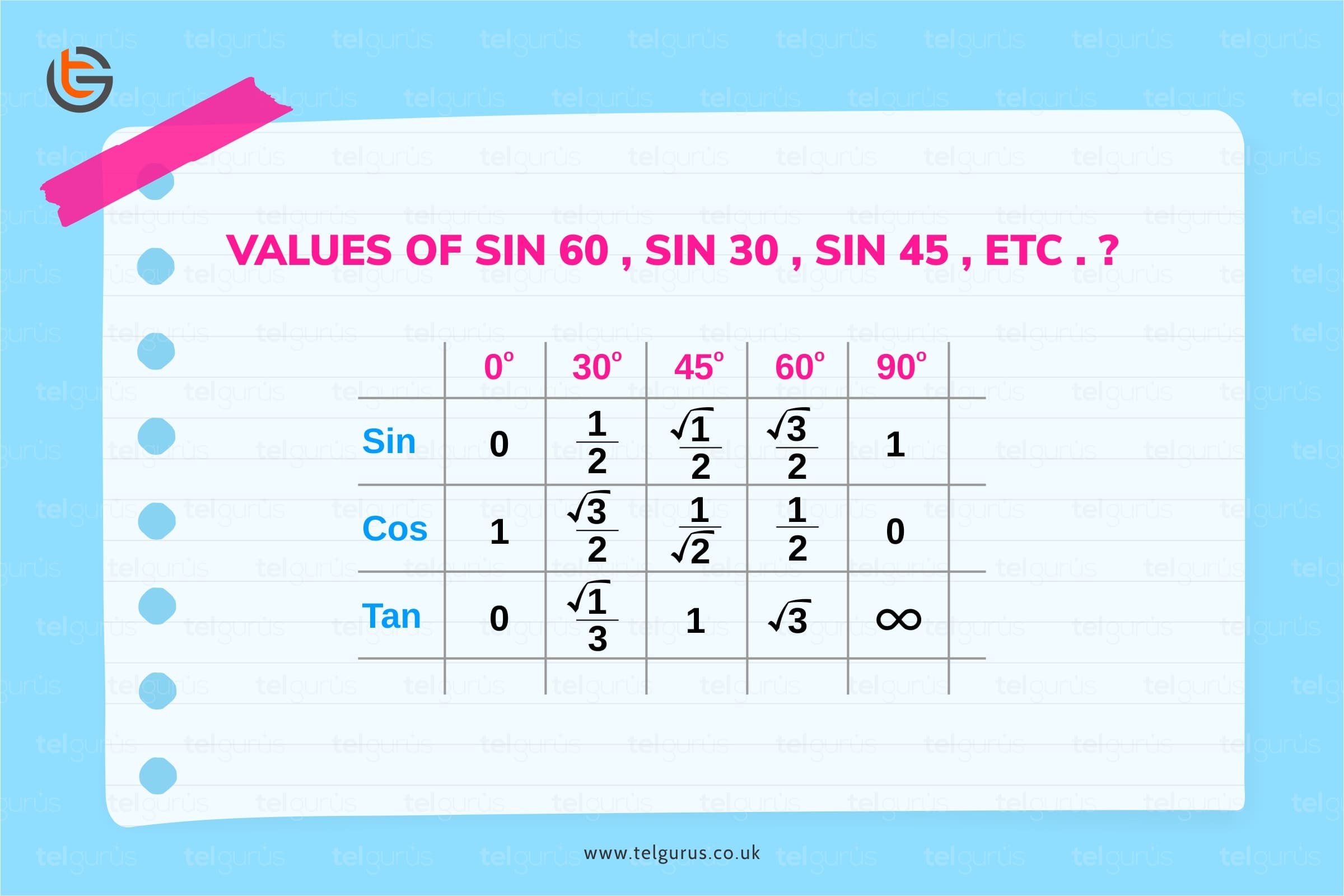
There are mainly five angles that you need to focus, these are 0°, 30°, 45°, 60° and 90°.

sin 0° = √ (0 / 4) = 0

sin 30° = √ (1 / 4) = 1 / 2

sin 45° = √ (2 / 4) = 1 / √ 2

sin 60° = √ (3 / 4) = √ 3 / 2

sin 90° = √ (4 / 4) = 1

So, in this way we can find the values of sine function.

The values of cosine or cos functions can be obtained by writing the values in the opposite direction. Let’s see how to learn them:

cos 0° = √ (4 / 4) = 1

cos 30° = √ (3 / 4) = √ 3 / 2

cos 45° =√ (2 / 4) = 1 / √ 2

cos 60° = √ (1 / 4) = 1 / 2

cos 90° = √ (0 / 4) = 0

This concludes that, the values of cos function are in the opposite direction of sine functions

sin 0° = cos 90°

sin 30° = cos 60°

sin 45° = cos 45°

sin 60° = cos 30°

sin 90° = cos 0°

Now, Let’s move to tangent functions

Tangent of an angle theta (θ) is obtained by dividing sin of that angle by cos of the same angle.

This means, tan θ = sinθ / cosθ

Therefore we can find the values of tan functions with the help of values of sin and cos functions.

This comes out to be:

Tan 0° = sin 0° / cos 0° = 0 / 1 = 0

Tan 30° = sin 30° / cos 30° = ( 1 / 2 ) / ( √ 3 / 2 ) = 1 / √ 3

Tan 45° = sin 45° / cos 45° = ( 1 / √ 2 ) / ( 1 / √ 2 ) = 1

Tan 60° = sin 60° / cos 60° = ( √ 3 / 2 ) / ( 1 / 2 ) = √ 3

Tan 90° = sin 90° / cos 90° = 1 / 0 = ∞ that means not defined or infinity.

Similarly, we can find the values of cosec functions by taking the reciprocals of respective sine function, values of secant functions by taking the reciprocals of cosine functions and that of cotangent by the reciprocals of tangent function.

So, we can see that just by finding the values of sine function we can easily find the values of other trigonometric functions.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development