What does congruent mean in math?

Book A Demo Class

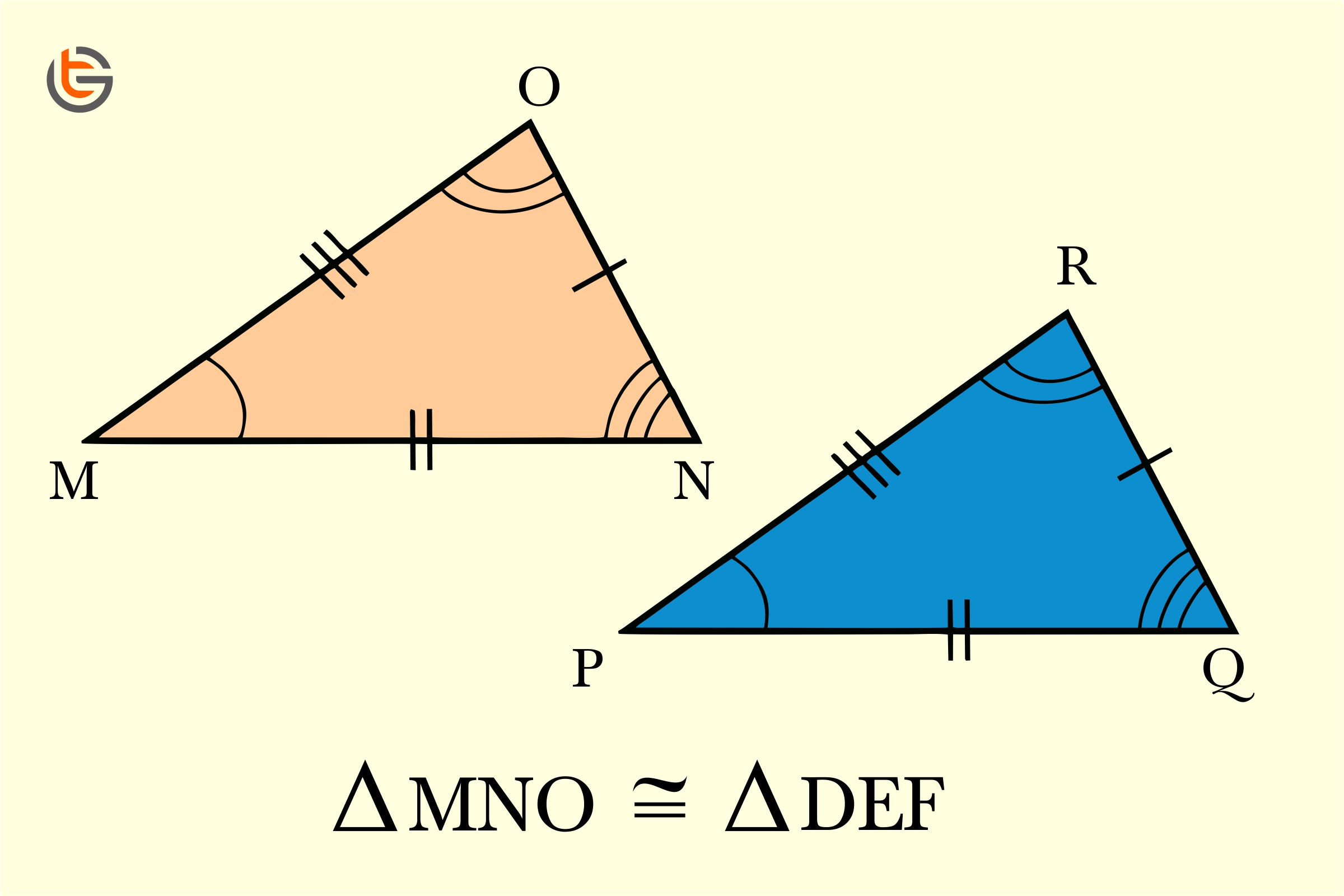
In Maths, the term congruent refers to those shapes or figures which can be flipped or repositioned to coincide with the other shapes. In other words, congruent means identical in size and shape. There are different theorems which are associated with the concept of congruency.

For example, for line segments, congruency means that they are equal in length or measure. For angles, the two angles are congruent only if both have same angle measures. Similarly, two triangles can be congruent if their corresponding parts are equal.

Let us understand with a practical example.

Draw two circles of same radius on a piece of paper. Cut both the circles out of papers and match them completely one on another. We notice that since both are of same shape and size, they completely overlap each other and thus, can be considered as congruent. The congruent is normally depicted a symbol “≅” meaning that two things are congruent to each other.

Thus, the word congruence can be used to describe relation between two objects or figures that are of same shape & size. Two geometrical figures can be considered congruent if they exactly superimpose on each other.

In above figures, both rectangles are of equal shape and can exactly superimpose on one other, thus, the two rectangles defined as A&B are congruent or in other words, A≅B.

Properties of Congruence:

There are three properties of congruence as listed below:

Reflexive property
Symmetric property
Transitive property

Reflexive Property:

In geometry, reflexive property means that a line segment or an angle or a shape is congruent to itself. For example, ∠Z ≅ ∠Z for any angle Z

Symmetric property:

This property means that if one geometrical figure is congruent to the other figure, then the second one is also congruent to the first figure. Consider that there are two angles ∠Z &∠Y. As per this property, if ∠Z ≅ ∠Y, then, the vice versa i.e. ∠Y ≅ ∠Z.

Transitive property:

This property states that if two shapes, angles or lines are congruent to the third one, then, the first two are congruent to each other. For example, If X ≅ Y and Y ≅ Z, then X ≅ Z.

Congruence of Triangles:

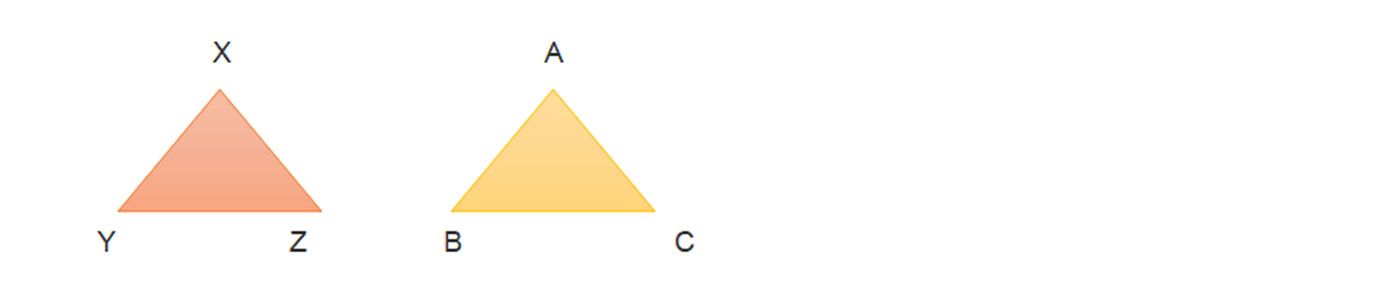
Two triangles are said to be congruent to each other if their sides are of equal length and their angles are equal in measures. Also, both these can be superimposed on each other.

As clear from the above figures, Δ ABC and Δ XYZ are the congruent triangles, as the corresponding sides and corresponding angles in both the triangles are equal.

The vertices: A and X, B and Y, and C and Z are the same.
The sides: XY = AB, YZ=BC and XZ=AC;
The angles: ∠X = ∠A, ∠Y = ∠B, and ∠Z = ∠C.

Thus, Δ ABC ≅ Δ XYZ

For finding two triangles are congruent or not, there are different ways as listed below:

In following listed ways, we can work upon to find if two triangles are congruent: