What is a chord in math?

Book A Demo Class

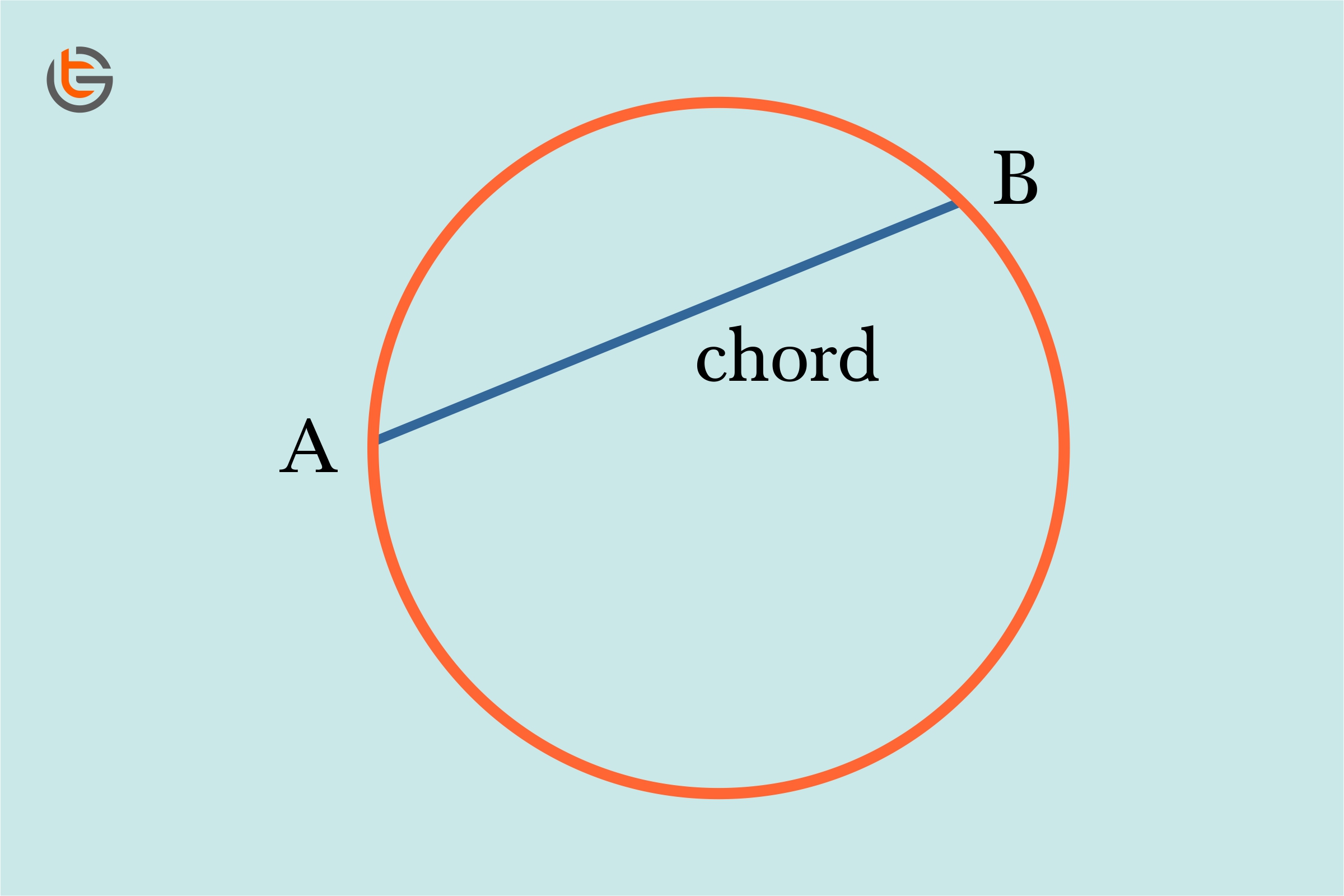
Chord: Chord is the line segment that joins the two points on the circumference of the circle or we can say on the boundary of circle.

Let us take an example to make the concept more clear.

Example:

In the above figure, AB is the chord which joins the two points on the circumference of the circle. Not only AB is the chord of the circle but all the line segments that join any two points on the circumference or boundary of the circle will make the chords of that circle.

Longest Chord

Any line that passes through the center and whose end points lie on the circle will be of the maximum length. Longest chord is that chord which passes through the center of the circle that is also called the diameter of the circle. So, diameter is the longest chord of the circle.

We can say that all diameters are the chords of the circle but all chords are not the diameters of the circle. Only that chord is termed as a diameter which passes through the center of the circle.

In the above circle AB is the chord as well as the diameter of the circle as it passes through the center of the circle while CD is only the chord of the circle not the diameter as it doesn’t passes through the center of the circle.

Properties of chord of circle:

The chords that are equal in length subtend equal angles at the center.
Perpendicular from the center of a circle to a chord bisects a chord.
The chords of a circle that are equal in length are always equidistant from the center.
Diameter is the longest chord of the circle.

So, chord is the line segment that joins the two points on the circumference of the circle.

Till now, we have understood the concept of chord, difference between chord & diameter and properties of chord.

Now, Let’s learn how to measure a chord’s length and discuss about the methods to find the length of chord.

Methods to find length of chord:

Method 1: using radius and perpendicular distance

Chord Length= 2 × √(r² – d²)

Where r is the radius and d is the perpendicular distance from the center of the circle to the chord.

Example:

Problem 1: Find the length of chord of circle where radius is 5 cm and perpendicular distance from the center to the chord is 4cm?

Solution:

Given radius, r =5 cm

distance, d =4 cm

using the formula, Chord length =2 × √(r² – d²)

=2 × √(5² – 4²)

=2 × √25-16

=2 × √9

=2 x 3

= 6 cm

Length of the chord is 6 cm.

Method 2: Using trigonometry

Chord Length=2 x r x sin(c / 2)

Where, r is the radius and c is the angle subtended at the center of the circle by the chord.

Some Important Points

The length of chord is inversely proportional to the perpendicular distance from center. It increases when the distance decreases.
The diameter is the longest chord of circle, whereby the perpendicular distance from center to chord is zero.
Two radii joining the ends of chord to the center of circle form an isosceles triangle.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development