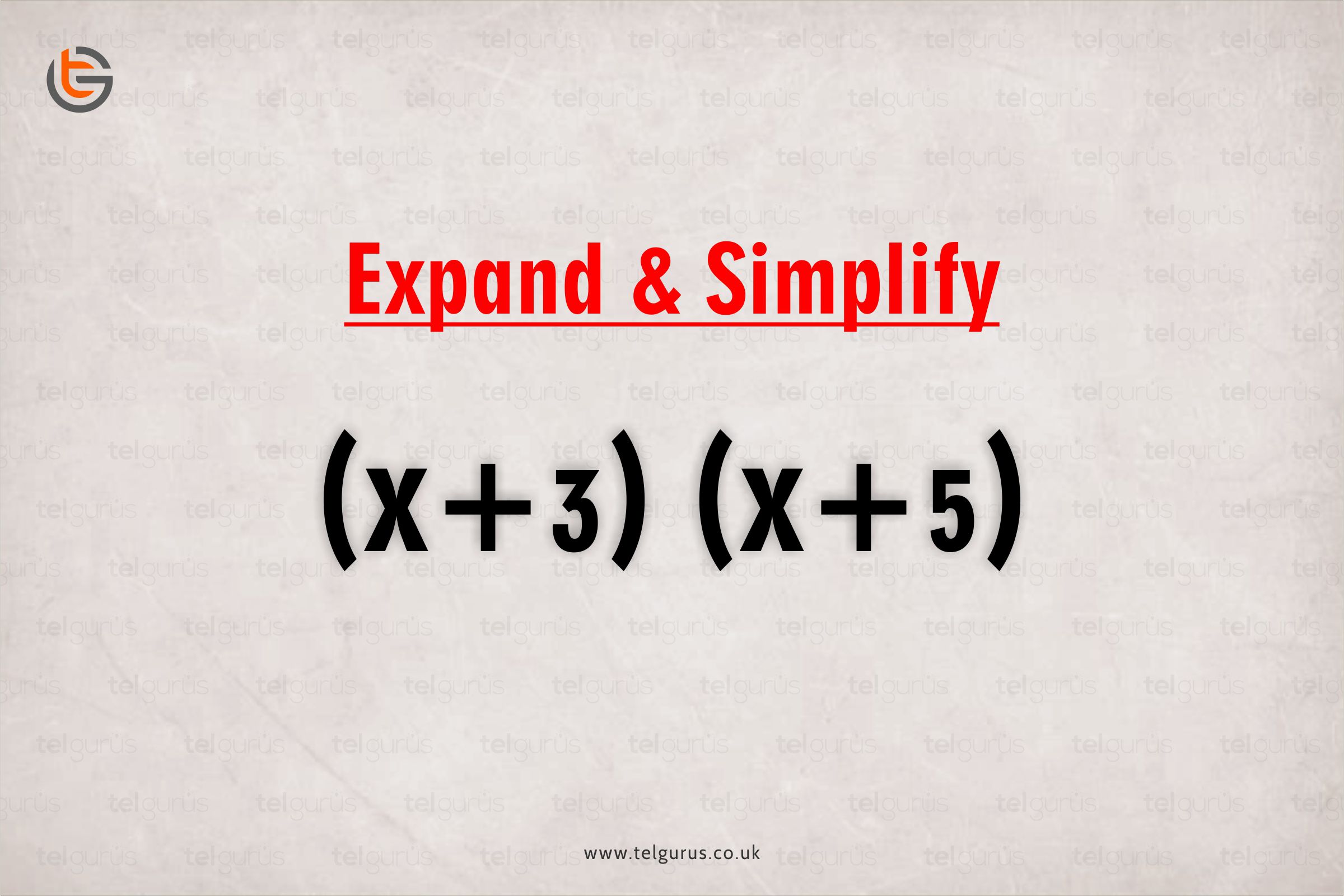Expand and simplify (x+2)(x+3)

Book A Demo Class

To solve (x + 2) (x + 3), there are mainly two methods. Both the methods are very simple.

While multiplying algebraic terms you need to be very careful about the signs. Multiplying two unlike signs will result in a negative term while multiplying two similar signs will always yield a positive term.

Solve a few of them using these methods and you will easily master these.

The two methods are:

Using distributive property
Using FOIL method

Let’s discuss them one by one:

Solving (x+2) (x+3) using distributive Property.

According to distributive properly, we have to first distribute the second term w.r.t. the first term.

So, let’s distribute:

x (x + 3) + 2 (x + 2)

Now, open the brackets one by one by multiplying

= x.x + 3.x + 2 (x + 2)

= x² + 3x + 2.x + 2.2

= x² + 3x + 2x + 4

Now, combining the Like terms we get:

= x² + (3x + 2x) + 4

= x² + 5x + 4

So, we the answer as (x+2) (x+3) = x² + 5x + 4

Now, let’s move on to second method

Solving (x+2) (x+3) using FOIL Method

FOIL method is one of the quickest method to simplify the algebraic expressions.

Before that you need to understand the meaning of FOIL. It means

F: Multiple first two terms of each bracket.

O: Multiple outer two terms.

I: Now, multiple inside two terms

L: multiply last two terms.

Then, collect all the like terms and add them.

Let’s solve step by step:

Applying FOIL on (x + 2) (x + 3) means

F: multiplying x from first bracket and x from second bracket. This gives x.x = x².

O: multiplying x from first bracket and 3 from second bracket gives 3x.

I: multiplying 2 from first bracket and x from second bracket gives 2x.

L: on multiplying the last two terms from each bracket gives 2 multiply by 3 = 6

So, we get the four terms as x², 2x, 3x and 6.

Now, It’s time to separate them as per like terms and add them.

x² + (2x + 3x) + 6

Here 2x and 3x are like terms with only one x. There is no more term for x² and also there is only one constant term i.e. 6.

So, on adding the coefficients of x we get :

= x² + 5x + 4

Whatever method you follow the answer would come out to be the same.

The FOIL method is pretty easy to learn as well as a great way to master the concepts. The more you use this formula, you speed of solving these algebraic terms will amplify.