Enrich your knowledge with our informative blogs
Expand and simplify (x+3)(x+5)
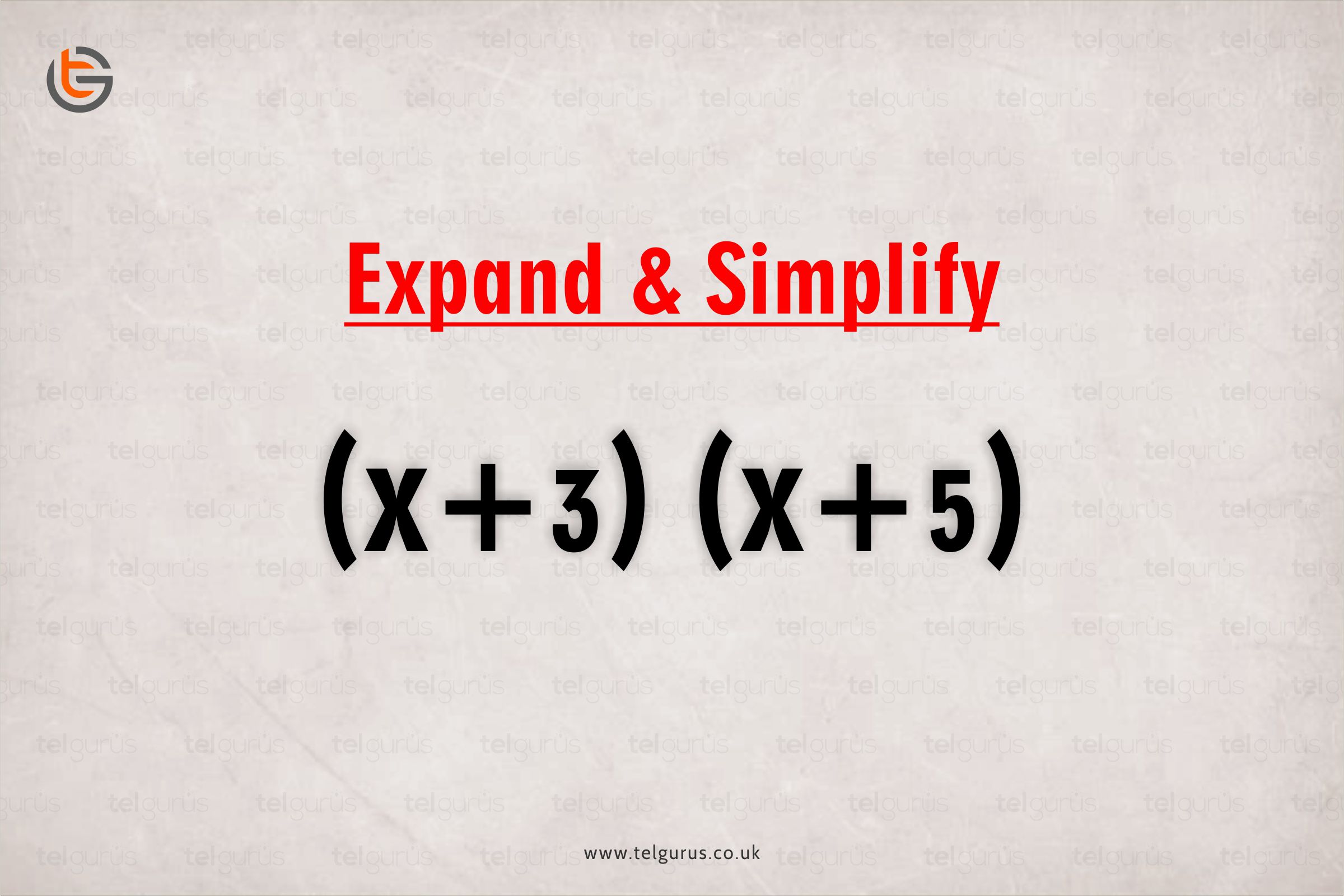
Algebra is one of the pillars of mathematics that needs a sound understanding and mastering of concepts to ace it.
Simplification of expressions is one of the most commonly asked questions from algebra that help you change complex terms into simpler ones or compact forms.
What is an algebraic expression?
It’s a mathematical term that is a mixed bag of variables and constants joined together with mathematical operators such as +, – , / and *.
So, Let’s see the various methods to solve (x + 3) (x +5).
While solving any mathematical expression, always follow the concept of BODMAS which states the order of mathematical operations.
Always start with opening brackets followed by solving division, multiplication, addition and then at last subtraction.
Book Your 60-minutes Free Trial class NOW!
There are mainly three methods of solving any algebraic expression involving brackets.
- Using FOIL Method
- Using Distributive property
- Direct formula
So, let’s discuss them one by one in detail.
1. Using FOIL Approach
FOIL approach is basically used by most of the students to simplify the algebraic expression. It’s an acronym that helps you remember the sequence of multiplication.
After multiplication, just sort the like terms and then just add.
What does FOIL stand for?
F: Multiply the first two terms of the expression
O: Multiple outer two terms of each bracket.
I: Now, multiple inside two terms.
L: multiply the last two terms from the bracket
Let’s apply this FOIL approach to our question (x + 3) (x + 5)
As per F, lets multiply first term from both brackets i.e. x in both cases. This comes out to be \displaystyle x.x={{x}^{2}}.
Moving on to O, we multiply the outer two terms i.e. x and 5 which comes out to be 5x.
I mean multiplying inner two terms i.e. 3 and x. On multiplying this becomes 3x.
Last, as per “L”, we multiply 3 and 5, the last two terms that give you 5 * 3 = 15.
So, we get the four terms as x^2, 5x, 3x and 15.
Let’s separate the like terms and add all these terms.
\displaystyle {{x}^{2}}+(5x+3x)+15= \displaystyle {{x}^{2}}+8x+15
So, on simplifying (x + 3)(x + 5) we get \displaystyle {{x}^{2}}+8x+15
2. Using Distributive property
You can simplify the algebraic expressions by using the distributive property.
How it works:
(x + a) (x + b) = x (x + b) +a (x+ b)
By using the above property, we multiply the second bracket with every element of first bracket.
(x + 3)(x + 5)
= x (x + 5) + 3 (x + 5)
= x.x + x.5 + 3.x + 3*5 (on opening the brackets)
= \displaystyle {{x}^{2}}+5x+3x+15
So, by combining the like terms we get our final answer
= \displaystyle {{x}^{2}}+8x+15
Book Your 60-minutes Free Trial class NOW!
3. Direct formula
The above two methods are best when you are going for subjective papers.
When you are aiming at competitive exams where every second matters, you just can’t afford to go for a long method.
We have a formula, you just need to substitute the values and that’s it.
You get the answer within a blink of an eye.
For solving (x + a) (x + b), use the formula x^2 + (a + b)x + ab
As per our question, the values of a and b are 3 and 5 respectively.
So, substituting them in the formula we get
= \displaystyle {{x}^{2}}+(3+5)x+3*5
= \displaystyle {{x}^{2}}+8x+15
The third was one was pretty easy and can be used to simplify the problem very quickly and efficiently.
Book Your 60-minutes Free Trial class NOW!
Read More – Mathematics Questions
View More – Useful links for Your Child’s Development

Unleash the Power of visualization to break tough concepts
Wanna be the next Maths wizard? Discover the new way of learning concepts with real-life Visualization techniques and instant doubt resolutions.
Categories
Recent Posts
- List of the qualities you should look for in your tutors?
- What is the most useful formulas in math?
- Describe the process of eating to defecation of food?
- Difference between the natural and artificial active response by the immunology system.
- Explain the different circle theorems
- How are nerve cells adapted to their function?










