What is a coefficient in math?

Book A Demo Class

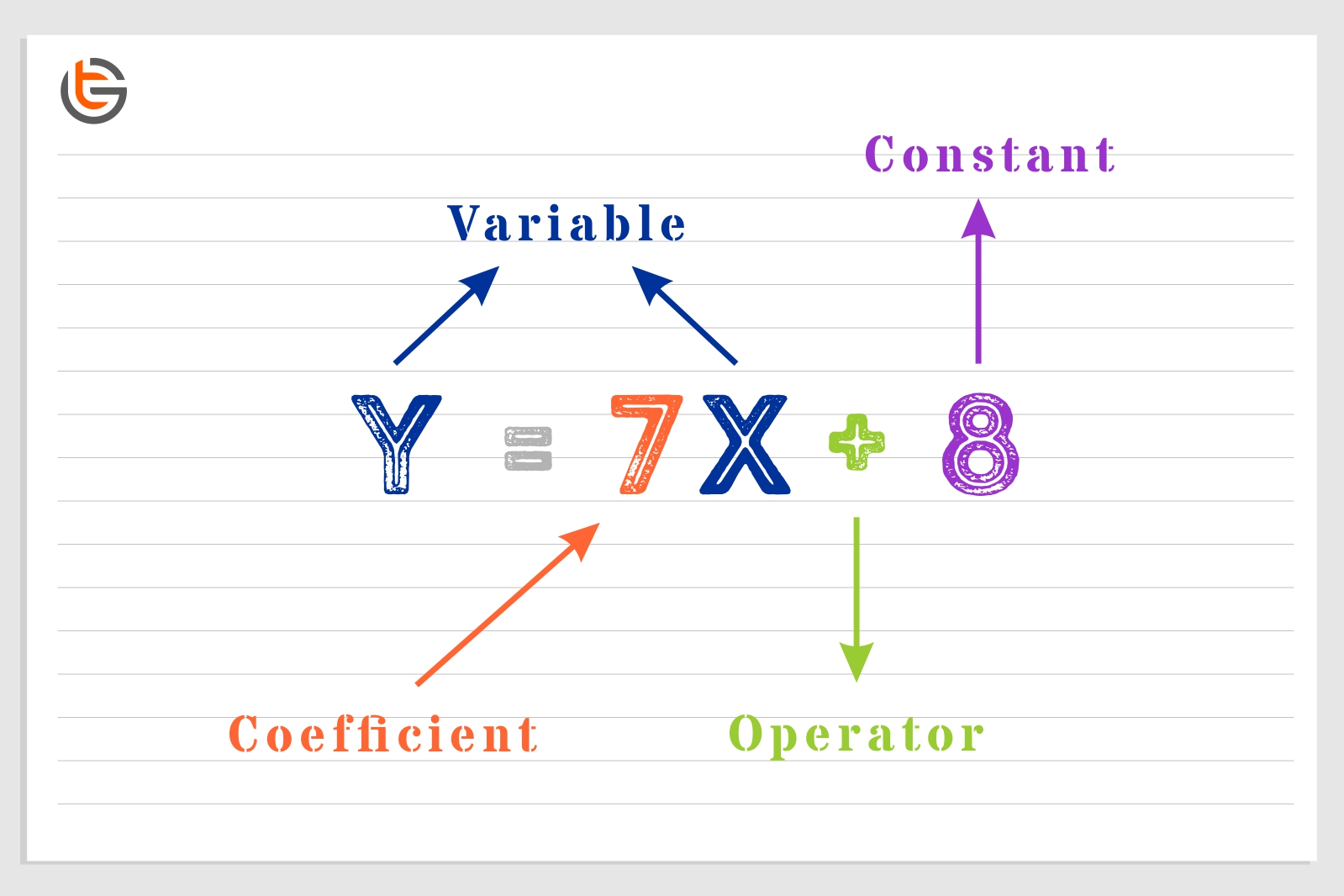
A coefficient is basically defined as an integer which is multiplied with the variable of a single term or the terms of a polynomial. In other words, it refers to a number or quantity placed with a variable. The variables having no number with them are assumed to have 1 as their coefficient.

What is a polynomial?

Poly means ‘many’

Nomial means ‘terms’

A mathematical expression having one or more algebraic terms is called a polynomial. Commonly it is expressed as a sum of several terms having different powers of same variable or variables.

Let us understand with few examples.

In an expression: ${ax+bx+z}$

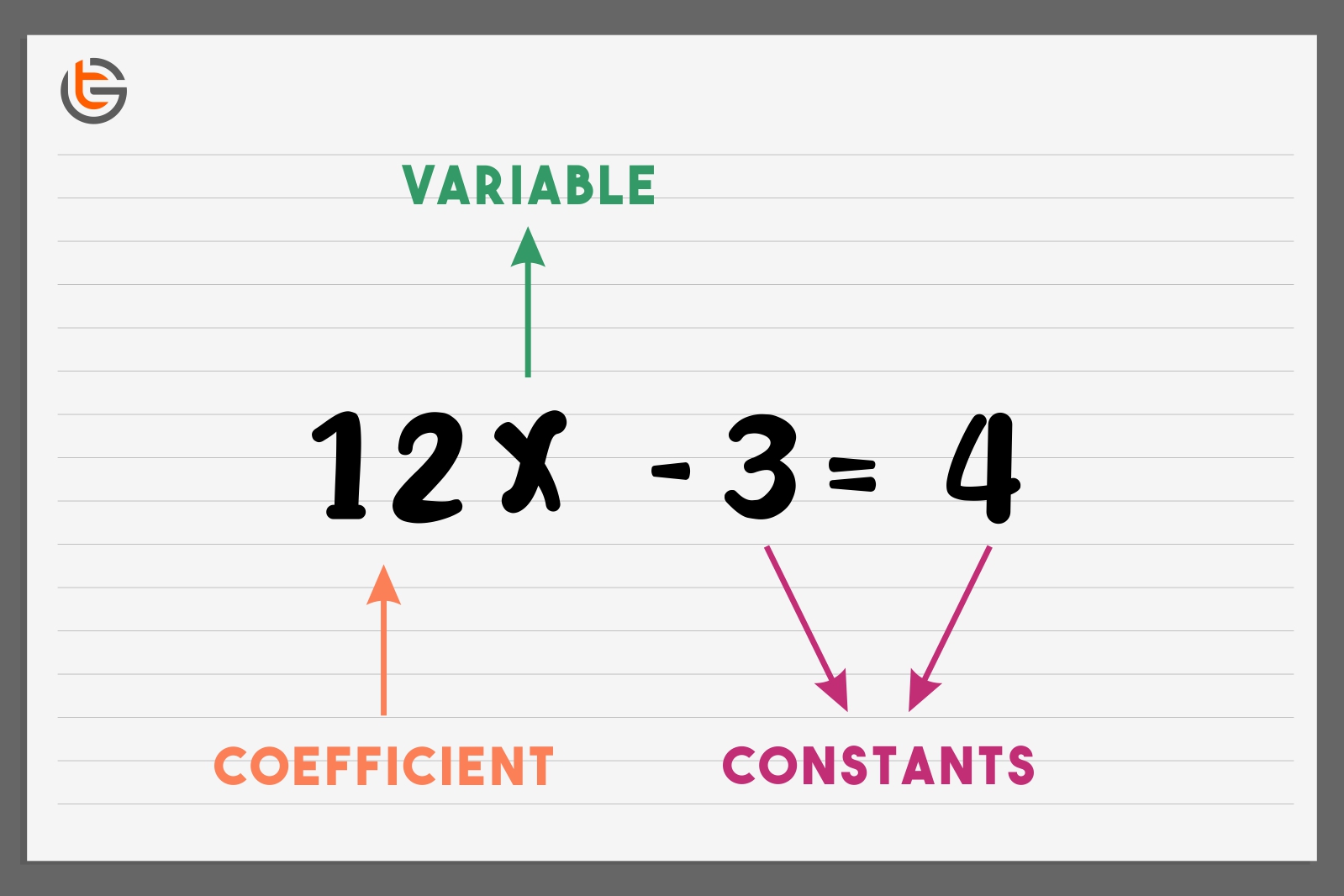
Here, is called variable and “a” and “b” are the coefficients and z is called constant.

In an expression: ${{x}^{2}}+5$ , 1 is the coefficient of ${{x}^{2}}$ .

Now, to identify a coefficient, it should be remembered that it always comes with a variable. In above example of ${ ax+bx+z, x}$ is the variable. Hence, ‘a’ and ‘b’ are the coefficient here.

Characteristics of a Coefficient:

A coefficient can be a real/imaginary, positive/negative or even in the form of fractions or decimals.

For example:

In an expression:

7x, 4.7 is the coefficient of variable x
In $\frac{{-1}}{2}y,\,\,\frac{{-1}}{2}$ is the coefficient of variable y.

Important Points to remember while working on coefficients:

A coefficient is always attached to a variable, whether variable is a single term or a polynomial.
In case there is no number or numerical factor in a term, the coefficient of the same is considered a 1.
The value of the variable is never the same and varies with a situation or according to the question.
The value of a constant is always fixed and cannot be changed.
A coefficient can never be zero because when we multiply 0 (as a coefficient) with any variable, the value of the same results into 0.
While adding or subtracting polynomials, coefficients of the same variables can only participate in these arithmetic operations. But there is no such rule for multiplication and division.

For example :

On adding $8{{x}^{2}}+12y+9$ and 17x²– 3y + 4

We get, (8 + 17) x² + (12 – 3) y + (9 + 4)

The answer becomes 25x²+ 9y + 13

Examples:

Find out the numerical Coefficients in the term : $\frac{{2xy2}}{7}$

Solution: $\frac{2}{7}$ is the coefficient of the above term.

Find out the numerical coefficients in the following algebraic expression: 7x²– 5y + 8.

Solution: Here we have three algebraic terms. In the term 7x², the numerical coefficient of the term 7x²is 7, -5 the coefficient of y, and 8 is a constant. Therefore, the numerical coefficients are 7and -5.

Find out the numerical coefficients in the expression: $9{{a}^{2}}-3y+8$

Solution: Amongst these three algebraic terms, the numerical coefficient of the term $~9{{a}^{2}}$ is 9, -3 is the coefficient of y, and 8 is a constant. Therefore, the numerical coefficients are 9 and -3.

Find out the numerical coefficients in the expression: $7{{w}^{2}}+8e+5$

Solution: In the term $7{{w}^{2}}$ the numerical coefficient of the term $7{{w}^{2}}$ is 7, 8 is the coefficient of e, and 5 is a constant. Therefore, the numerical coefficients are 7 and 8.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development