What is absolute value in math?

• Book A Demo Class

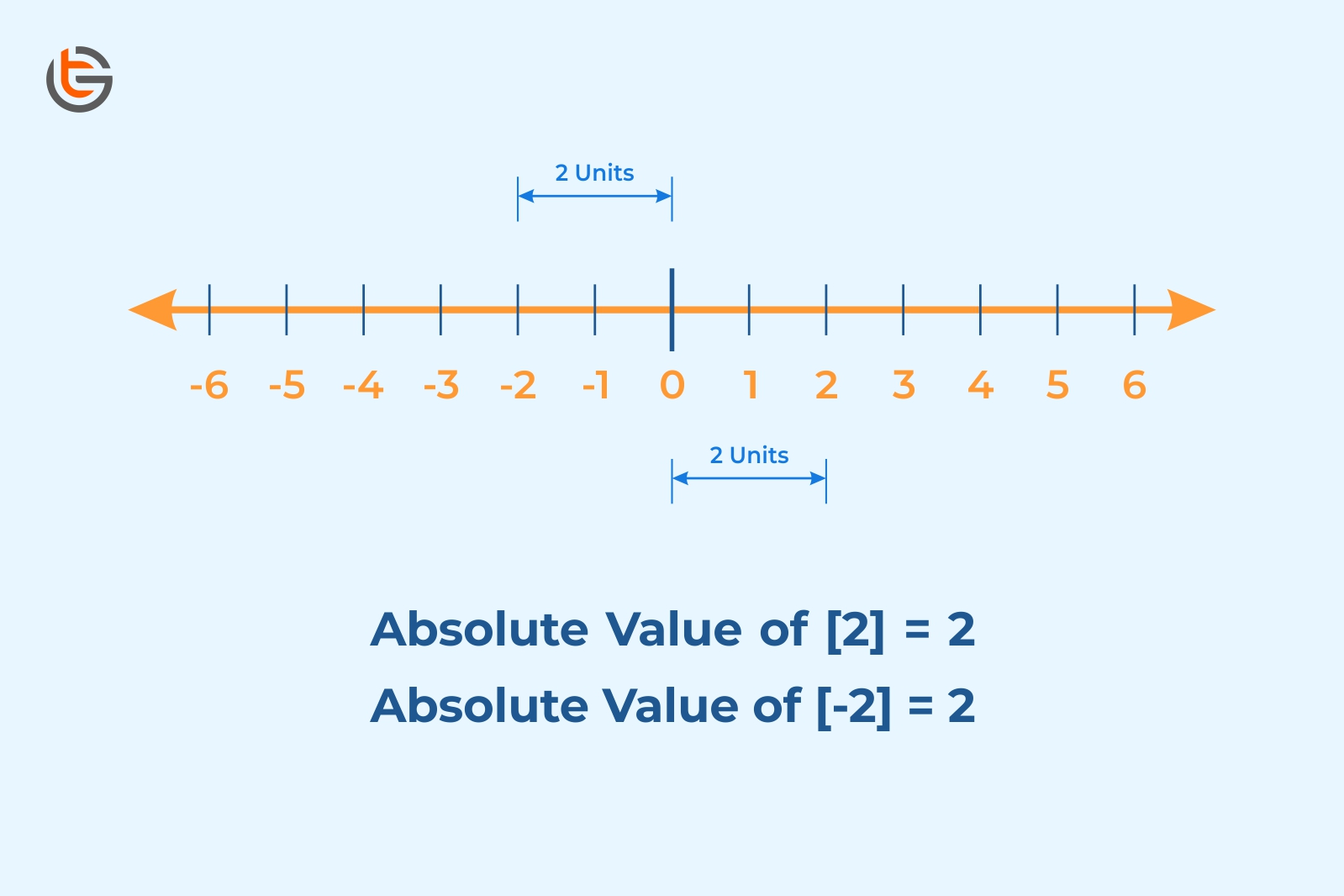
Absolute value: In mathematics, absolute value is a number or value that tells the given number’s distance from 0 on the real number line.

As the distance is always positive, the absolute value of every number is always non-negative irrespective of the integer value.

It is also known as the magnitude of the given number. The symbol used to represent the absolute value is two vertical bars, i.e.  | x | or also known as modulus of x.

Formula for finding Absolute Value of Real Numbers

| x | =    {  x    if x > or equal to zero }

{  -x  if x<o  }

The symbol | x| is pronounced as modulus of x . Modulus is a Latin word that means ‘measure’. The modulus of any vector quantity is taken as positive and is its absolute value. Also quantities like distance, volume, price, time are always represented as absolute values.

As we have discussed above that absolute value is always non negative. Sometimes a sign is attributed to a numeric value to signify the direction in addition to the value. But for absolute value, the sign of the numeric value is ignored and only the numeric value is considered.

In the above number line if we take for example absolute value of 4 is 4 and absolute value for -4 is also 4. This means the distance of -4 and 4 is 4 units from zero on the number line and we know that distance can never be negative.

i.e. | 4 | = 4

|-4 | = – (-4) = 4    (by using the formula stated above)

Some Important points:

• The absolute value of x is represented by either |x| or abs(x).
• The absolute value of any no. always results in a non negative value.
• We pronounce |x| as modulus of x.

Examples:

Find the absolute value of

• -|-14| = -14
• |12| = 12
• |-5| = 5

Properties of Absolute Value:

1.       Non – negativity:

|x| ≥ zero

2.       Positive – definiteness

|x| = 0 ∀  a = 0   (∀ means for all)

3.       Multiplicativeness:

|x * y | = |x|  *   |y|

4.       Sub-additivity:

|x + y| ≤ |x| + |y|

5.       Symmetry:

|-x| = |x|

6.       Identity of indiscernible:

|x – y| = 0 ∀  a = b

7.       Preservation of division:

| x \ y| =  |x| \ |y|

8.        Equivalent to sub-additivity:

|x – y| ≥    |  |x| – |y|  |

Absolute value of Complex Number

Complex numbers consist of a real and an imaginary part. Hence, unlike integers, finding the absolute value of complex numbers isn’t that easy.

Suppose: x + iy is the given complex number where x is the real part and iy is the imaginary part

z = x + iy;

The absolute value of z will be;

|z|= square root of [Re(z)^2 + Im(z)^2]

|z|=square root of x^2 + y^2

Where x and y are real numbers and ^ is the power.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development 

Unleash the Power of visualization to break tough concepts

Wanna be the next Maths wizard? Discover the new way of learning concepts with real-life Visualization techniques and instant doubt resolutions.

Book A Demo Class

• 

  What does increased mean in math?

• 

  What is a multiple in math?