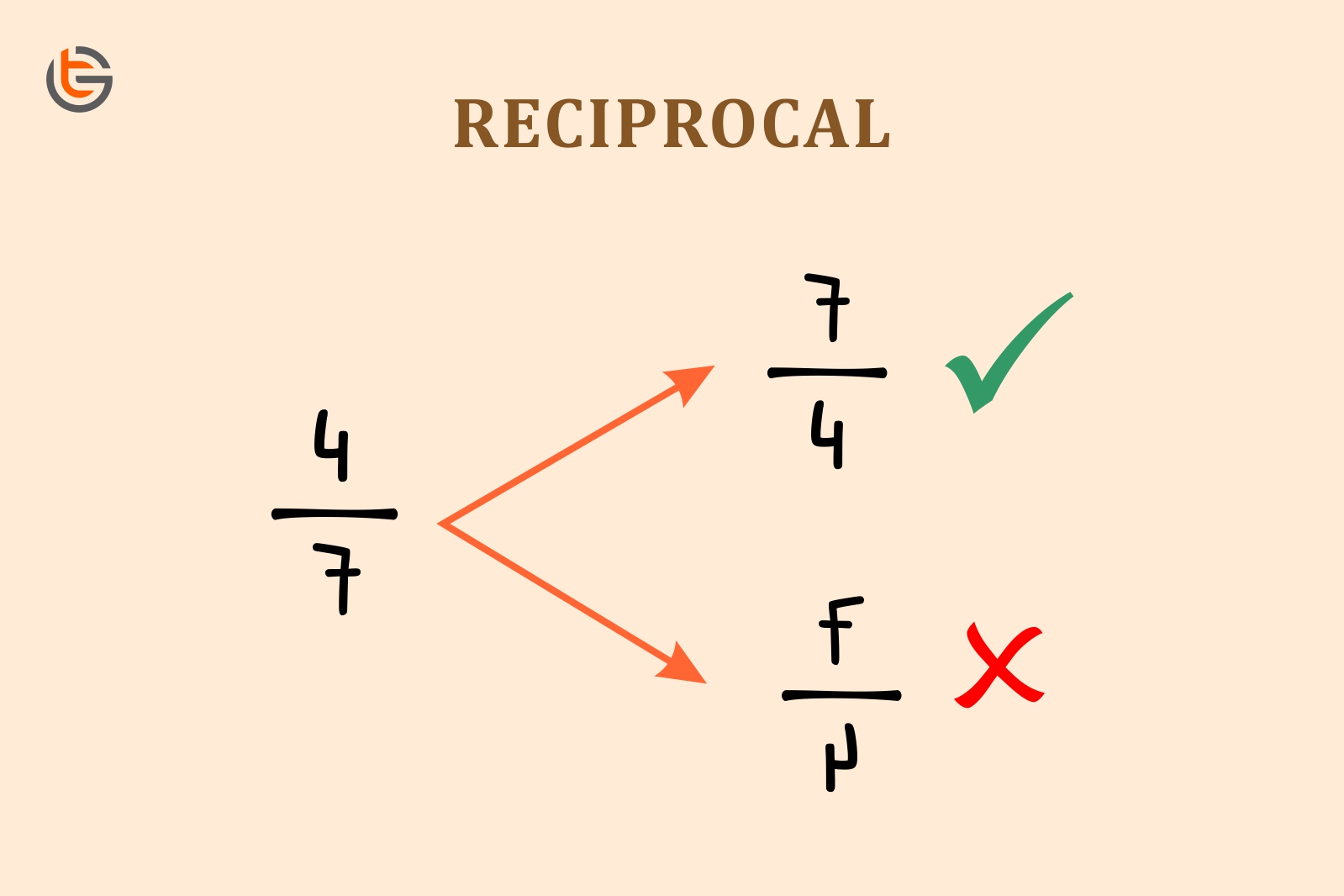
What is a reciprocal in math?

Book A Demo Class

Definition

Reciprocal in math is a mathematical number which when multiplied by the given number gives product as 1.

For example: Reciprocal of 23 will be 1/23.

The word reciprocal has been derived from the Latin word “reciprocus” which means returning. In other words, when we take the given number as a multiplier and its reciprocal as multiplicand, the product comes out to be 1. It is also known as inverted number or multiplicative inverse of a number.

How to find a reciprocal of a number?

Reciprocal of a given number is obtained by taking an inverse of it or dividing 1 by that number. We can easily obtain the reciprocal of a natural number, negative number, decimal number as well as fractions.

Reciprocal of a number ‘x’ is written as 1/x or x^-1.

Reciprocal of a natural number

Let us assume x be a natural number, it’s reciprocal will be written as 1/x.

Steps to do it:

Step1: Turn the number into a fraction by making the numerator as the number and the denominator as 1.

Step2: Now, interchange numerator and denominator. This means number becomes denominator and 1 gets placed in the numerator.

Problem: Find the reciprocal of 39.

Solution: The reciprocal of 39 is 1/39.

Reciprocal of an integer

If x is an integer where x is not equal to 0, the inverse or reciprocal of x is 1/x. For a negative number say -y, the reciprocal becomes -1/y.

Problem: Find the reciprocal of -45.

Solution: The reciprocal of 45 is -1/45.

Reciprocal of a decimal number

Just like integers, the multiplicative inverse of a decimal number can be obtained by writing 1 over it.

Problem: Find the reciprocal of 9.6.

Solution: The reciprocal of 9.6 is 1/9.6.

Reciprocal of a fraction

A fraction comprises of numerator and denominator. For obtaining reciprocal o a fraction, just interchange the upper and lower part of the fraction. This means if a fraction is m/n, its inverse becomes n/m.

Problem: Find the reciprocal of 13/11.

Solution: The reciprocal of 13/11 is 11/13.

After taking reciprocal of a fraction, the improper fraction becomes a proper fraction and vice versa.

Taking inverse of a mixed fraction

We, all know a mixed fraction comprises of a whole number and a fraction. To take the reciprocal of a mixed number, first, convert the mixed number into an improper fraction and then take its inverse.

Let’s first convert mixed number to an improper fraction. For that, multiply the whole number with the denominator of the fraction and then add the numerator to it. This number becomes the numerator and denominator stays as it is.

Problem: Find the reciprocal of $5\frac{{11}}{{20}}$

Solution: Let’s convert $5\frac{{11}}{{20}}$ into mixed fraction.

Numerator = (5 x 20) + 11 = 100 + 11 = 111

Denominator = 20

Your fraction becomes $\frac{{111}}{{20}}$

Now, it’s easy to take reciprocal of a fraction which is $\frac{{20}}{{111}}$ .

Some important points to remember

Zero is the only number that does not has a reciprocal because any number when multiplied by zero gives 0.
The product of a reciprocal and the number is always unity.
Taking reciprocal of a reciprocal number will give back the original number.
Reciprocal of a number is also termed as turning the number upside down.

Read More – Mathematics Questions

View More – Useful links for Your Child’s Development